Лики божественной гармонии. Часть 3.
Алексей Стахов (20/09/2013)
Соавтор: Иван Райлян
Аннотация
Выдающийся русский философ Алексей Лосев, исследователь эстетики античности и эпохи Возрождения, в следующих словах сформулировал «золотую» парадигму древних греков: «С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения». Новейшие открытия современной науки, основанные на Платоновых телах, золотом сечении, числах Фибоначчи: фуллерены, Нобелевская Премия – 1996; квазикристаллы, Нобелевская Премия – 2011; экспериментальное доказательство существования гармонии «золотого сечения» в квантовом мире; обнаружение фибоначчиевой закономерности в таблице Менделеева; «гипотеза Прокла» и новый взгляд на «Начала» Евклида и историю развития математики, начиная с Евклида; гиперболические фунции Фибоначчи и новая геометрическая теория филлотаксиса; треугольник Паскаля и обобщенные числа Фибоначчи; обобщенные золотые пропорции и закон структурной гармонии систем; лямбда-числа Фибоначчи как новый класс целочисленных последовательностей, обладающих уникальными математическими свойствами; «металлические пропорции» и общая теория гармонических гиперболических функций; решение четвертой проблемы Гильберта и поиск гармонических гиперболических миров Природы; "золотые" матрицы, преобразования Фибоначчи-Лоренца и «золотая» интерпретация специальной теории относительности; «золотые» геноматрицы; алгоритмическая теории измерений, коды и компьютеры Фибоначчи; системы счисления с иррациональными основаниями, троичная зеркально-симметричная арифметика и "золотая" теория чисел как новое направление в теории чисел; обобщенные матрицы Фибоначчи и новая теория кодирования; наконец, «математика гармонии» как новое междисциплинарное направление, восходящее к «Началам» Евклида, - все это «лики божественной пропорции» в современной науке, которые создают общую картину ее движения к "Золотой" Научной Революции, что в совокупности отражает одну из важнейших тенденций в развитии современной науки – возврат к Пифагору, Платону и Евклиду.
Часть III
«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».
Бертран Рассел
Предисловие
Каждому из нас не раз приходилось задумываться над тем, почему Природа способна создавать такие удивительные эстетические структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие? В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Что такое «гармония»? И имеет ли она математическое выражение? Для моделирования «мира гармонии» в античном мире, прежде всего в Древней Греции, была создана математика гармонии, элементы которой возрождены в современной науке во многих книгах [1 - 25], включая книгу Alexey Stakhov “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science”, опубликованной в 2009 г. одним из наиболее престижных научных издательств мира “World Scientific” [25].
Цель настоящей публикации, предназначенной для широкой аудитории, состоит в том, чтобы популярно объяснить понятие «гармонии», которое было введено в науку на заре развития человеческой цивилизации, рассказать об истории этого направления в античный период, эпоху средневековья, эпоху Возрождения, в 19 и 20 веках, а также ввести в круг идей и приложений современной «математики гармонии», автивно развивающейся в 21 в. [25]. Конечно, «математика гармонии» - это раздел математики; поэтому полностю избежать математических формул в статье, посвященной этой математической дисциплине, авторам не удалось. Однако, «математика гармонии» - это достаточно простая (можно сказать, «элементарная») математика, в которой используются математические формулы, доступные школьникам старших классов. И авторы надеются на снисхождение наших читателей.
Статья состоит из 4-х частей:
Часть III. Платоновы тела, «гипотеза Прокла», новый взгляд на «Начала» Евклида, фуллерены и квазикристаллы
Часть IV. Роль «математики гармонии» в развитии современной науки
Часть III. Платоновы тела, «гипотеза Прокла», новый взгляд на «Начала» Евклида, фуллерены и квазикристаллы
7. Платоновы тела
Правильные многоугольники и многогранники
Человек проявляет интерес к правильным многоугольникам и многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа.
Что же такое многоугольник и многогранник? Для ответа на этот вопрос напомним, что собственно геометрию определяют иногда как науку о пространстве и пространственных фигурах – двумерных и трехмерных. Двумерную фигуру можно определить как множество отрезков прямых, ограничивающих часть плоскости. Такая плоская фигура называется многоугольником. Из этого следует, что многогранник можно определить как множество многоугольников, ограничивающих часть трехмерного пространства. Многоугольники, образующие многогранник, называются его гранями.
Издавна ученые интересовались идеальными или правильными многоугольниками, то есть, многоугольниками, имеющими равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которое может ограничить часть плоскости. Общую картину интересующих нас правильных многоугольников наряду с равносторонним треугольником составляют: квадрат (четыре стороны), пентагон (пять сторон), гексагон (шесть сторон), октагон (восемь сторон), декагон (десять сторон) и т.д. Очевидно, что теоретически нет каких-либо ограничений на число сторон правильного многоугольника, то есть, число правильных многоугольников бесконечно.
Что же такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? На первый взгляд ответ на этот вопрос очень простой – столько же, сколько существует правильных многоугольников. Однако это не так. В «Началах Евклида» мы находим строгое доказательство того, что существует только пять выпуклых правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны.
Правильные многогранники в «Началах» Евклида
Теории многогранников посвящено много книг. Одной из наиболее известных является книга английского математика М. Веннинджера «Модели многогранников» [39]. Книга начинается с описания так называемых правильных многогранников, то есть, многогранников, образованных простейшими правильными многоугольниками одного типа. Эти многогранники принято называть Платоновыми телами, названными так в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии. Мы начнем наше рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники (Рис.21).
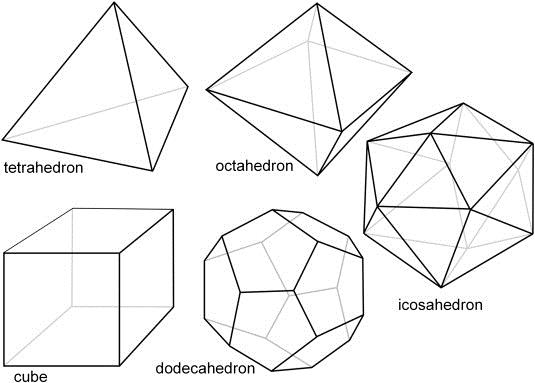
Рис.21. Платоновы тела: тетраэдр (tetrahedron), октаэдр (octahedron), куб (cube) додекаэдр (dodecaedron), икосаэдр (icosahedron)
Первым (и простейшим) среди правильных многогранников является тетраэдр (tetrahedron). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников.
Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром (octahedron). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основанием. Если соединить две такие пирамиды основаниями, то получится симметричное тело с восемью треугольными гранями – октаэдр (octahedron).
Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится фигура с 20 треугольными гранями – икосаэдр (icosahedron).
Следующая правильная форма многоугольника – квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом (cube).
Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника – пентагона. Если собрать 12 пентагонов таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще одно Платоново тело, называемое додекаэдром (dodecahedron).
Следующим правильным многоугольником является шестиугольник. Однако если соединить три шестиугольника в одной точке, то мы получим плоскость, то есть, из шестиугольников нельзя построить объемную фигуру. Любые другие правильные многоугольники выше шестиугольника не могут образовывать тел вообще. По существу мы повторили рассуждения, которые провел Евклид в Книге XIII своих «Начал». Именно эта книга посвящена изложению завершенной геометрической теории Платоновых тел. И именно из этих рассуждений вытекает, что существует только пять выпуклых правильных многогранников, гранями которых могут быть только равносторонние треугольники, квадраты и пентагоны.
Числовые характеристики Платоновых тел. Основными числовыми характеристиками Платоновых тел является число сторон грани m, число граней n, сходящихся в каждой вершине, число граней Г, число вершин В, число ребер Р и число плоских углов У на поверхности многогранника Эйлер открыл и доказал знаменитую формулу:
В - Р + Г = 2 ,
связывающую число вершин, ребер и граней любого выпуклого многогранника. Указанные выше числовые характеристики приведены в Табл.2.
Таблица 2. Числовые характеристики Платоновых тел
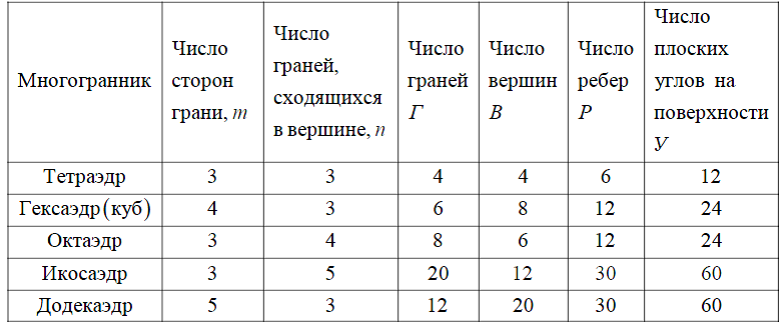
Уместно обратить внимание на свойство дуальности, которое связывет Платоноваы тела. Из Табл.2 вытекает, что для гексаэдра (куба) и октаэдра число ребер Р=12 и число плоских углов на поверхности У=24 совпадают. Но число граней Г=6 куба совпадает с числом вершин В=6 октаэдра, а число вершин куба В=8 совпадает с числом граней Г=8 октаэдра. Кроме того, число сторон грани куба m=4 совпадает с числом граней октаэдра, сходяшимся в вершине, n=4, при этом число граней куба, сходящимся в n=3, совпадает с числом сторон грани октаэдра m=3. Подобная же сиуация наблюдается и в случае икосаэдра и додкаэдра. В таких случаях говорят о дуальности соответствующих Платновых тепл, то есть, куб дуален октаэдру, а икосаэдр дуален додекаэдру. Заметим, что в свойстве дуальности отражена «скрытая» гармония Платоновых тел.
Золотое сечение в додекаэдре и икосаэдре. Додекаэдр (dodecahedron) и дуальный ему икосаэдр (icosahedron) занимают особое место среди Платоновых тел. Прежде всего, необходимо подчеркнуть, что геометрия додекаэдра и икосаэдра непосредственно связана с золотым сечением. Действительно, гранями додекаэдра являются пентагоны, то есть, правильные пятиугольники, основанные на золотом сечении. Если внимательно посмотреть на икосаэдр, то можно увидеть, что в каждой его вершине сходится пять треугольников, внешние стороны которых образуют пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что золотое сечение играет определяющую роль в конструкции этих двух Платоновых тел.
Но существуют более глубокие подтверждения глубокой математической связи золотого сечения с икосаэдром и додекаэдром. И эта связь приводит к тому, что додекаэдр и икосаэдр выражают в «скрытой» форме гармонию золотого сечения.
9. Гипотеза Прокла: новый взгляд на «Начала» Евклида и историю развития математики
С какой целью Евклид написал свои «Начала»?
На первый взгляд, кажется, что ответ на этот вопрос очень простой: главная цель Евклида состояла в том, чтобы изложить основные достижения греческой математики за 300 лет, предшествующих Евклиду, используя «аксиоматический метод» изложения материала. Действительно, «Начала» Евклида являются главным трудом греческой науки, посвященным аксиоматическому построению геометрии и математики. Такой взгляд на «Начала» наиболее распространен в современной математике.
Однако, кроме «аксиоматической» точки зрения существует и другая точка зрения на мотивы, которыми руководствовался Евклид при написании «Начал». Эта точка зрения высказана греческим философом и математиком Проклом Диадохом (412-485), одним из первых комментаторов «Начал».
Прежде всего, несколько слов о Прокле. Прокл родился в Византии в семье богатого адвоката из Ликии. Намереваясь пойти по стопам отца, подростком уехал в Александрию, где учился сначала риторике, затем заинтересовался философией и стал учеником александрийского неоплатоника Олимпиодора Младшего. Именно у него Прокл начал изучать логические трактаты Аристотеля. В возрасте 20 лет Прокл переезжает в Афины, где Платоновскую Академию в то время возглавлял Плутарх Афинский. Уже к 28-летнему возрасту Прокл написал одну из своих главнейших работ, комментарий на платоновского «Тимея». Около 450 г. Прокл становится главой Платоновской Академии.
Среди математических сочинений Прокла наиболее известным является его «Комментарий к первой книге «Начал» Евклида». В этом Комментарии он выдвигает следующую необычную гипотезу, которую называют “гипотезой Прокла”. Суть ее состоит в следующем. Как известно, XIII-я, то есть, заключительная книга «Начал», посвящена изложению теории пяти правильных многогранников, которые играли главенствующую роль в «Космологии Платона» и в современной науке известны под названием Платоновых тел. Именно на это обстоятельство и обращает внимание Прокл. Как подчеркивает Эдуард Сороко [3], по мнению Прокла, Евклид «создавал «Начала» якобы не с целью изложения геометрии как таковой, а чтобы дать полную систематизированную теорию построения пяти «Платоновых тел», попутно осветив некоторые новейшие достижения математики».
Значение гипотезы Прокла для развития математики. Главный вывод из «гипотезы Прокла» состоит в том, что «Начала» Евклида, величайшее греческое математическое сочинение, было написано Евклидом под непосредственным влиянием греческой «идеи Гармонии», которая была связана с Платоновыми телами. Таким образом, «гипотеза Прокла» позволяет высказать предположение, что хорошо известные в античной науке "Пифагорейская доктрина о числовой гармонии Мироздания» и «Космология Платона», основанная на правильных многогранниках, были воплощены в величайшем математическом сочинении греческой математики, “Началах” Евклида. С этой точки зрения мы можем рассматривать “Начала” Евклида как первую попытку создать «Математическую теорию гармонии мироздания», которая ассоциировалась в античной науке с Платоновыми телами. И это было главной идеей греческой науки! Это и есть главная тайна «Начал» Евклида, которая приводит к пересмотру истории возникновения математики, начиная с Евклида.
К сожалению, оригинальная гипотеза Прокла, касающаяся истинных целей, которые преследовал Евклид при написании Начал, проигнорирована многими современными историками математики, что привело к искаженному взгляду на структуру математики и всего математического образования. И это является одной из главных «стратегических ошибок» в развитии математики.
«Гипотеза Прокла» и «ключевые» проблемы античной математики. Как известно, академик Колмогоров в книге [33] выделил две главные, то есть, «ключевые» проблемы, которые стимулировали развитие математики на этапе ее зарождения - проблему счета и проблему измерения. Однако, из «гипотезы Прокла» вытекает еще одна «ключевая» проблема – проблема гармонии, которая была связана с «Платоновыми телами» и «золотым сечением» - одним из важнейших математических открытий античной математики (Предложение II.11 «Начал» Евклида). Именно эта проблема была положена Евклидом в основу «Начал», главной целью которых было создание геометрической теории «Платоновых тел», которые в «космологии Платона» выражали гармонию Мироздания. Эта идея приводит к новому взгляду на историю математики, представленному на Рис.22.
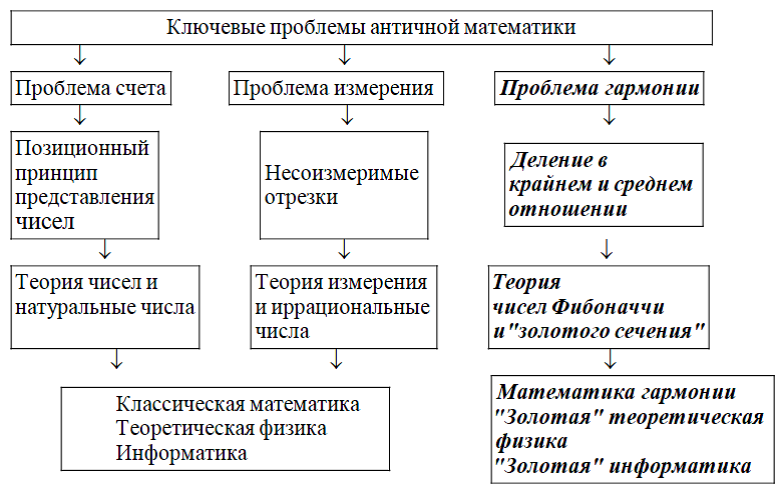
Рис. 22. «Ключевые» проблемы античной математики и новые направления в математике, теоретической физике и информатике
Подход, демонстрируемый с помощью Рис.22, впервые был изложен в работе [40]. Он основан на следующих рассуждениях. Уже на этапе зарождения математики было сделано ряд важных математических открытий, которые фундаментально повлияли на развитие математики и всей науки в целом. Важнейшими из них являются:
1. Позиционный принцип представления чисел, сделанный вавилонскими математиками во 2-м тысячелетии до н.э. и воплощенный ими в Вавилонской 60-ричной системе счисления. Это важное математическое открытие лежит в основе всех последующих позиционных систем счисления, в частности, десятичной системы и двоичной системы - основы современных компьютеров. Это открытие, в конечном итоге, привело к формированию понятия натурального числа – важнейшего понятия, лежащего в основе математики.
2. Доказательство существования несоизмеримых отрезков. Это открытие, сделанное в научной школе Пифагора, привело к переосмысливанию ранней пифагорейской математики, в основе которой лежал «принцип соизмеримости величин», и к введению иррациональных чисел – второго (после натуральных чисел) фундаментального понятия математики. В конечном итоге, эти два понятия (натуральные и иррациональные числа) и были положены в основу «Классической Математики».
3. Деление отрезка в крайнем и среднем отношении («золотое сечение»). Описание этого математического открытия дано в «Началах» Евклида (Предложение II.11). Это предложение было введена Евклидом с целью создания полной геометрической теории «Платоновых тел» (в частности, додекаэдра), изложению которых посвящена заключительная (XIII-я) книга «Начал» Евклида.
Сформулированный выше подход (Рис.22) приводит к выводу, который может оказаться неожиданным для многих математиков. Оказывается, что параллельно с «Классической Математикой» в науке, начиная с древних греков, начало развиваться еще одно математическое направление – «Математика Гармонии», которая, как и классическая математика, восходит к «Началам» Евклида, но акцентирует свое внимание не на «аксиоматическом подходе», а на геометрической «задаче о делении отрезка в крайнем и среднем отношении» (Предложение II.11) и на теории правильных многогранников, изложенной в Книге XIII «Начал» Евклида. В развитии «математики гармонии» в течение нескольких тысячелетий принимали участие выдающиеся мыслители, ученые и математики: Пифагор, Платон, Евклид, Фибоначчи, Пачоли, Кеплер, Кассини, Бине, Люка, Клейн, а в 20-м веке – известные математики Коксетер, Воробьев, Хоггатт и Вайда. И мы никак не можем игнорировать этот исторический факт.
10. Додекаэдро-икосаэдрическая доктрина
Истоки доктрины
Согласно замечанию комментатора последнего издания сочинений Платона, у него «вся космическая пропорциональность покоится на принципе золотого деления, или гармонической пропорции». Как упоминалось, космология Платона основывается на правильных многогранниках, называемых телами Платона. Представление о «сквозной» гармонии мироздания неизменно ассоциировалось с ее воплощением в этих пяти правильных многогранниках, выражавших идею повсеместного совершенства мира. И то, что главная «космическая» фигура - додекаэдр, символизировавший тело мира и вселенской души, был основан на золотом сечении, придавало последнему особое очарование, смысл главной пропорции мироздания.
Космология Платона стала началом так называемой икосаэдро-додекаэдрической доктрины, которая с античных пор красной нитью проходит через всю человеческую науку. Суть этой доктрины состоит в том, что додекаэдр и икосаэдр есть типичные формы природы во всех ее проявлениях, начиная с космоса и заканчивая микромиром.
Форма Земли
Вопрос о форме Земли постоянно занимал умы ученых античных времен. И когда гипотеза о шарообразной форме Земли получила подтверждение, возникла идея о том, что по своей форме Земля представляет собой додекаэдр. Так, уже Сократ писал:
«Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из 12 кусков кожи».
Эта гипотеза Сократа нашла дальнейшее научное развитие в трудах физиков, математиков и геологов. Так, французский геолог де Бимон и известный математик Пуанкаре считали, что форма Земли представляет собой деформированный додекаэдр.
Российский геолог С. Кислицин, также разделял мнение о додекаэдрической форме Земли. Он высказал гипотезу о том, что 400-500 млн. лет назад геосфера додекаэдрической формы превратилась в гео-икосаэдр. Однако такой переход оказался неполным и незавершенным, в результате чего гео-додекаэдр оказался вписанным в структуру икосаэдра. Более подробная информация об этой гипотезе изложена в книге [19].
Тайна Египетского календаря
Одним из первых солнечных календарей был египетский, созданный в 4-м тысячелетии до н.э. Первоначально египетский календарный год состоял из 360 дней. Год делился на 12 месяцев ровно по 30 дней в каждом. Однако позже было обнаружено, что такая длительность календарного года не соответствует астрономическим данным. И тогда египтяне добавили к календарному году еще 5 дней, которые, однако, не считались днями месяцев. Это были 5 праздничных дней, соединявших соседние календарные годы. Таким образом, египетский календарный год имел следующую структуру: 365=12 х 30+5. Заметим, что именно египетский календарь является прообразом современного календаря.
Возникает вопрос: почему египтяне разделили календарный год на 12 месяцев? Ведь существовали календари с другим количеством месяцев в году. Например, в календаре майя год состоял из 18 месяцев по 20 дней в месяце. Следующий вопрос, касающийся египетского календаря: почему каждый месяц имел ровно 30 дней (точнее суток)? Можно поставить некоторые вопросы и по поводу системы измерения времени, которая, воможно, была сформирована в более поздние времена. В частности, возникает вопрос: почему единица часа была выбрана таким образом, чтобы она ровно 24 раза укладывалась в сутки, то есть, почему 1 сутки = 24 (2 х 12) часа? Далее: почему 1 час = 60 минут, а 1 минута = 60 секунд? Эти же вопросы относятся и к выбору единиц угловых величин, в частности: почему окружность разбита на 360°, то есть, почему 2p=360°=12 х 30°? К этим вопросам добавляются и другие, в частности: почему астрономы признали целесообразным считать, что существует 12 зодиакальных знаков, хотя на самом деле в процессе своего движения по эклиптике Солнце пересекает 13 созвездий? И еще один «странный» вопрос: почему вавилонская система счисления имела весьма необычное основание – число 60?
Анализируя египетский календарь, а также системы измерения времени и угловых величин, мы обнаруживаем, что в них с удивительным постоянством повторяются четыре числа: 12, 30, 60 и производное от них число 360 = 12´30. Возникает вопрос: не существует ли какой-то фундаментальной научной идеи, которая могла бы дать простое и логичное объяснение использованию этих чисел в египетском календаре и системах?
Обратимся к додекаэдру (Рис.21). Из Табл.1 вытекает, что додекаэдр имеет 12 граней, 30 ребер и 60 плоских углов на своей поверхности. Каково же было удивление древних египтян, когда они обнаружили, что этими же числами выражаются циклы Солнечной системы, а именно, 12-летний цикл Юпитера, 30-летний цикл Сатурна и, наконец, 60-летний цикл Солнечной системы. Таким образом, между такой совершенной пространственной фигурой, как додекаэдр, и Солнечной системой, существует глубокая математическая связь! Такой вывод сделали античные ученые. Это и привело к тому, что додекаэдр был принят в качестве «главной фигуры», которая символизировала Гармонию Мироздания. Поскольку по представлению древних движение Солнца по эклиптике имело строго круговой характер, то, выбрав 12 знаков Зодиака, дуговое расстояние между которыми равнялось ровно 30°, египтяне удивительно красиво согласовали годичное движение Солнца по эклиптике со структурой своего календарного года: один месяц соответствовал перемещению Солнца по эклиптике между двумя соседними знаками Зодиака! Более того, перемещение Солнца на один градус соответствовало одному дню в египетском календарном году! При этом эклиптика автоматически получалась разделенной на 360°. Позже эта же научная идея была использована создателями системы измерения времени. Разделение каждой половины суток на 12 частей (12 граней додекаэдра) привело к введению часа– важнейшей единицы времени. Разделение часа на 60 минут (60 плоских углов на поверхности додекаэдра) привело к введению минуты – следующей важной единицы времени. Точно также была введена секунда (1 минута = 60 секунд).
Таким образом, выбрав додекаэдр в качестве главной «гармонической» фигуры мироздания, и строго следуя числовым характеристикам додекаэдра 12, 30, 60, ученым удалось построить чрезвычайно стройный календарь, а также системы измерения времени и угловых величин.
Вот такие удивительные выводы вытекают из сопоставления додекаэдра с Солнечной системой. И если наша гипотеза правильна (пусть кто-нибудь попытается ее опровергнуть), то отсюда следует, что вот уже много тысячелетий человечество живет под знаком «золотого сечения» (которое лежит в основе додкаэдра)! И каждый раз, когда мы смотрим на циферблат наших часов, который также построен на использовании числовых характеристик додекаэдра 12, 30 и 60, мы прикасаемся к главной «Тайне Мироздания» - золотому сечению, сами того не подозревая! Видимо, такая гипотеза Египетского календаря касается некоторой «скрытой» тайны Солнечной системы, связнной с «золотым сечением».
Иоганн Кеплер и Феликс Клейн
“Misterium Cosmographiсum”. Свою научную деятельность Иоганн Кеплер начал в небольшом австрийском городе Граце, куда после окончания Тюбингенской академии он был направлен преподавателем математики в гимназию.
Сделаем одно «лирическое отступение». С 15-го по 19-е июля 1996 года в Граце состоялась 7-я Международная конференция по числам Фибоначчи и их приложениям. На этой конференции Алексей Стахов сделал доклад “The Golden Section and Modern Harmony Mathematics”, с которого, по существу, и началось развитите современной «математики гармонии» как нового междисциплинарного направления современной науки [25]. Доклад вызвал большой интерес математиков-фибоначчистам и был отобран для публикации в сборнике «Applications of Fibonacci Numbers» (1998) [69]. В период пребывания в Граце проф. Алексей Стахов сфотографировался возле памятника Иоганну Кеплеру, установленному в одном из парков Граца.

Алексей Стахов рядом с памятником Иоганну Кеплеру
(Грац, июль 1996)
Первым астрономическим сочинением Кеплера, написанным в Граце, была небольшая книжка со следующим названием: «Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пропорций между небесными кругами и истинных причин, числа и размеров небесных сфер, а также периодических движений, изложенных с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком из достославной провинции Штирии». Сам он называл эту книгу, опубликованную в 1597 г., «Misterium Cosmographicum» («Тайна космографии»).
Читая первое сочинение Кеплера «Misterium Cosmographicum» («Тайна космографии»), не устаешь удивляться его фантазии. Глубокое убеждение в существовании гармонии мира наложило отпечаток на все мышление Кеплера. Цель своих исследований, изложенных в «Тайне космографии», Кеплер сформулировал в предисловии:
«Любезный читатель! В этой книжке я вознамерился доказать, что всеблагой и всемогущий Бог при сотворении нашего движущегося мира и при расположении небесных орбит избрал за основу пять правильных тел, которые со времен Пифагора и Платона и до наших дней снискали столь громкую славу, выбрал число и пропорции небесных орбит, а также отношения между движениями выбрал в соответствии с природой правильных тел. Сущность трех вещей - почему они устроены так, а не иначе – особенно интересовали меня, а именно: число, размеры и движения небесных орбит».
Раскрыть тайну мироздания значило, по Кеплеру, ответить на вопрос, который он сам же себе и поставил впервые в истории астрономии. Именно в книжке «Тайна космографии» Кеплеру удалось, как ему казалось, раскрыть эту тайну. Ее сущность, по мнению Кеплера, состоит в следующем:
«Земля (орбита Земли) есть мера всех орбит. Вокруг нее опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфера Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг тетраэдра сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в него сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная в него сфера есть сфера Меркурия».
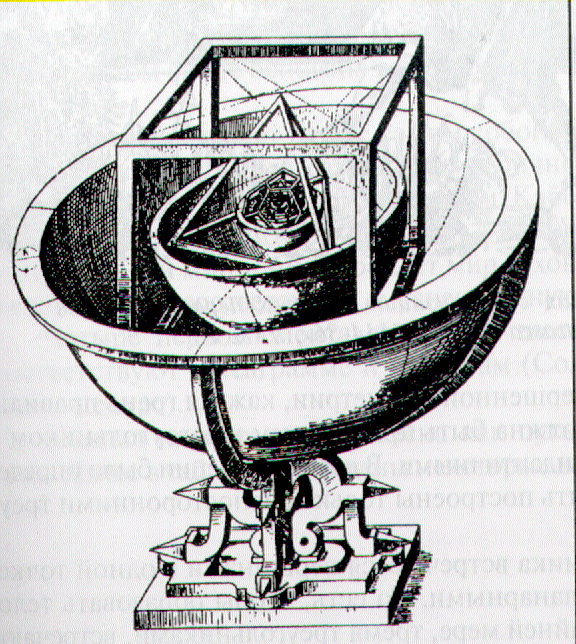
Рис. 23. «Космический кубок» – Кеплерова модель Солнечной системы
Знаменитый Кеплеров Космический кубок (Рис.23), вправляющий в Платоновы тела хрустальные сферы, воплощает эту модель в материи. Самое драгоценное достояние античной геометрии (Платоновы тела) встроено, наконец, в астрономию. Хотя эта модель, в конечном итоге, оказалась ошибочной, Кеплер никогда не отказывался от нее и считал эту модель одним из своих высших научных достижений. Уступая настояниям друзей, Кеплер на склоне лет предпринял второе издание своей первой книги «для пользы не только книготорговцев, но и ученых». В предисловии к новому изданию, подводя итог своим исканиям, Кеплер писал, что все его достижения вдохновлены «Misterium Cosmographicum» с его «Космическим кубком»:
«Мне самому, в течение вот уже 25 лет работающему над преобразованием астрономии, главы этой книжки не раз освещали путь. Почти все астрономические труды, которые я опубликовал за это время, берут свое начало в той или иной главе моей первой работы…»
Икосаэдр как главный геометрический объект математики. Как упоминалось, среди пяти Платоновых тел икосаэдр и додекаэдр занимают особое место. Эти два Платоновых тела непосредственно связаны с пентаклом, а через него – с золотой пропорцией. И наверное, нельзя считать случайным, что додекаэдро-икосаэдрическая доктрина получила неожиданное развитие в трудах выдающегося немецкого математика Феликса Клейна (1849 -1925).
Гениальность Феликса Клейна проявилась в том, что более чем 100 лет назад он сумел предсказать выдающуюся роль Платоновых тел, в частности, икосаэдра, в будущем развитии науки, в частности, математики. В 1884 г. Феликс Клейн опубликовал книгу «Лекции об икосаэдре и решении уравнений пятой степени» [41], посвященную геометрической теории икосаэдра.
Согласно Ф. Клейну, ткань математики широко и свободно разбегается листами отдельных теорий. Но есть объекты, в которых сходятся несколько листов, - своеобразные точки ветвления. Их геометрия связывает листы и позволяет охватить общематематический смысл разных теорий. Именно таким математическим объектом, по мнению Клейна, является икосаэдр. Клейн трактует икосаэдр как математический объект, из которого расходятся ветви пяти математических теорий: геометрия, теория Галуа, теория групп, теория инвариантов и дифференциальные уравнения.
В чем же состоит значение идей выдающегося математика с точки зрения теории гармонии? Прежде всего, в качестве объекта, объединяющего «главные листы» математики, выбрано «тело Платона» - икосаэдр, основанный на золотом сечении. Отсюда естественным образом мы можем сделать заключение, что именно золотое сечение и является той главной геометрической идеей, которая, согласно Клейну, может объединить всю математику. Заметим, что именно эта идея лежит в основе современной «математики гармонии» [25].
Современники Клейна не сумели по достоинству понять и оценить революционный характер «икосаэдрической» идеи Клейна. Ее значение было понято ровно через 100 лет, то есть только в 1984 г., когда израильский физик Дан Шехтман опубликовал заметку, подтверждающую существование специальных сплавов (названных квазикристаллами), обладающих так называемой «икосаэдрической» симметрией, то есть, симметрией 5-го порядка, что строго запрещено классической кристаллографией. В 2011 г. автор этого открытия Дан Шехтман был удостоен Нобелевской Премии в области химии.
Таким образом, еще в 19-м веке гениальная интуиция Феликса Клейна привела его к мысли о том, что одна из древнейших геометрических фигур – икосаэдр – является главной геометрической фигурой математики. Тем самым Клейн в 19 в. вдохнул новую жизнь в развитие «додекаэдро-икосаэдрического представления» о структуре Вселенной, последователями которого были великие ученые и философы: Платон, построивший свою космологию на основе правильных многогранников, Евклид, посвятивший, согласно «гипотезе Прокла», свои «Начала» изложению теории Платоновых тел, Иоганн Кеплер, использовавший Платоновы тела при создании своего Космического кубка, оригинальной геометрической модели Солнечной системы.
Правильные многогранники в природе и современной науке
Живая природа. В широко известной книге немецкого биолога начала 20-го века Э. Геккеля "Красота форм в природе" можно прочитать такие строки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".
Создания природы, приведенные в книге Геккеля, красивы и симметричны. Это неотделимое свойство природной гармонии. В книге приводятся примеры одноклеточных организмов, форма которых точно передает икосаэдр. Чем же вызвана такая природная геометризация? Может быть, тем, что из всех многогранников именно икосаэдр имеет наибольший обьем и наименьшую площадь поверхности. Это геометрическое свойство помогает морскому микроорганизму преодолевать давление водной толщи. Интересно и то, что именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.
Кристаллография. Правильные многогранники - самые «выгодные» фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли NaCl, монокристалл алюминиево-калиевых квасцов имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сурьмянистый сернокислый натрий - тетраэдра, бор - икосаэдра. Правильные многогранники определяют форму кристаллических решеток многих химических веществ.
Фуллерены. Но наиболее сенсационную информацию из области «додекаэдро-икосаэдрической доктрины» принес нам Нобелевский Комитет. В 1996 г. Нобелевская Премия по химии была присужена группе ученых (Р. Керл, Р. Смолли и Г. Крото) за открытие фуллеренов.
Термин «фуллерен» берет свое начало от имени американского архитектора Бакминстера Фуллера (1995-1983), который, оказывается, использовал подобные структуры при конструировании куполов зданий (еще одно применение усеченного икосаэдра!).
Центральное место среди фуллеренов занимает молекула С60, которая характеризуется наибольшей симметрией и как следствие наибольшей стабильностью. В этой молекуле, напоминающей покрышку футбольного мяча и имеющую структуру правильного усеченного икосаэдра (Рис.24), атомы углерода располагаются на сферической поверхности в вершинах 20 правильных шестиугольников и 12 правильных пятиугольников, так что каждый шестиугольник граничит с тремя шестиугольниками и тремя пятиугольниками, а каждый пятиугольник граничит с шестиугольниками.
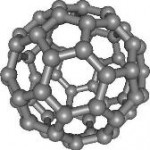

Рис.24. Молекула С60 и футбольный мяч
Квазикристаллы. 12 ноября 1984 г. в небольшой статье, опубликованной в авторитетном журнале «Physical Review Letters” израильским физиком Даном Шехтманом, было предъявлено экспериментальное доказательство существования металлического сплава с исключительными свойствами. При исследовании методами электронной дифракции этот сплав проявил все признаки кристалла. Его дифракционная картина составлена из ярких и регулярно расположенных точек, совсем как у кристалла. Однако эта картина характеризуется наличием «икосаэдрической» или «пентангональной» симметрии, строго запрещенной в кристалле из геометрических соображений. Такие необычные сплавы были названы квазикристаллами. Менее чем за год были открыты многие другие сплавы подобного типа. Их было так много, что квазикристаллическое состояние оказалось намного более распространенным, чем это можно было бы представить.
В чем же состоит методологическое значение открытия квазикристаллов? Прежде всего, открытие квазикристаллов является моментом великого торжества «додекаэдро-икосаэдрической доктрины», которая пронизывает всю историю естествознания и является источником глубоких и полезных научных идей. Во-вторых, квазикристаллы разрушили традиционное представление о непреодолимом водоразделе между миром минералов, в котором «пентагональная» симметрия была запрещена, и миром живой природы, где «пентагональная» симметрия является одной из наиболее распространенных. И не следует забывать, что главной пропорцией икосаэдра является «золотая пропорция». И открытие квазикристаллов является еще одним научным подтверждением, что, возможно, именно «золотая пропорция», проявляющая себя как в мире живой природы, так и в мире минералов, является одной из важнейших пропорций Мироздания.
Литература
-
Coxeter, H. S. M. Introduction to Geometry. New York: John Wiley and Sons, 1961.
-
Воробьев Н.Н. Числа Фибоначчи. М.: Наука, 1984. (первое издание - 1961).
-
Hoggat V. E. Jr. Fibonacci and Lucas Numbers. - Boston, MA: Houghton Mifflin, 1969.
-
Vajda S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. - Ellis Harwood Limited, 1989.
-
Huntley H. E. The Divine Proportion: a Study in Mathematical Beauty. Dover Publications, 1970.
-
Стахов А.П. Введение в алогоритмическую теорию измерения. М.: Советское радио, 1977.
-
Стахов А.П. Коды золотой пропорции. М.: Радио и связь, 1984.
-
Сороко Э.М. Структурная гармония систем. Минск: Наука и техника, 1984.
-
Grzedzielski Jan. Energetycno-geometryczny kod Przyrody. Warszawa: Warszwskie centrum studenckiego ruchu naukowego, 1986 (in Polen).
-
Васютинский Н.А. Золотая пропорция. М.: Молодая Гвардия», 1990.
-
Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. Три взгляда на гармонию природы. М.: Стройиздат, 1990.
-
Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов: Свит, 1994.
-
Dunlap R.A. The Golden Ratio and Fibonacci Numbers. World Scientific, 1997.
-
Коробко В.И. Золотая пропорция и проблемы гармонии систем. М.: Изд-во Ассоциации строительных вузов стран СНГ, 1998.
-
Шевелев И.Ш. Метаязык живой природы. М.: Воскресенье, 2000.
-
Kappraff Jay. Connections. The geometric bridge between Art and Science. Second Edition. Singapore, New Jersey, London, Hong Kong: World Scientific, 2001.
-
Kappraff Jay. “Beyond Measure. A Guided Tour Through Nature, Myth and Number”. Singapore, New Jersey, London, Hong Kong: World Scientific, 2002.
-
Olsen Scott. The Golden Section: Nature’s Greatest Secret. New York: Walker Publishing Company, 2006.
-
Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. Санкт-Петербург: Питер, 2006.
-
Шевелев И.Ш. Основы гармонии. Визуальные и числовые образы реального мира. М.: Луч, 2009.
-
HRH Charles The Prince of Wales. Harmony: A New Way of Looking at Our World. Harper Publisher, 2010.
-
Аракелян Грант. Теория ЛМФ и принцип золотого сечения. В 4 частях. Академия Тринитаризма, 2011 (электронная публикация).
-
Григорьев Ю., Мартыненко Г. Типология последовательностей Фибоначчи: Теория и приложения. Введение в математику гармонии. LAMBERT Academic Pudlishing Gmbh & Co.KG. Saarbruecken, Germany, 2012.
-
Волошинов А. В. Математика и искусство. М., Просвещение, 2000.
-
Stakhov A.P. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science. New Jersey, London, Singapore, Hong Kong: World Scientific, 2009.
-
Шестаков В.П. Гармония как эстетическая категория. М.: Наука, 1973.
-
Пьер Тейяр де Шарден. Феномен человека. Перевод и примечания Н.А.Садовского - М.: "Прогресс", 1965.
-
Дарио Салас Соммэр. Мораль XXI века. М.: Издательский дом «София», 2004.
-
Дарио Салас Соммэр. Развитие внутреннего мира. Москва: Научная книга, 2008.
-
Дарио Салас Соммэр, От Золотой Математики к Золотому Поведению //«Академия Тринитаризма», М., Эл № 77-6567, публ.15105, 20.02.2009
-
Дарио Салас Соммэр, А.П. Стахов, «Золотая» Герметическая Философия //«Академия Тринитаризма», М., Эл № 77-6567, публ.15144, 09.03.2009
-
Клайн М. Математика. Утрата определенности (пер. с англ.). Москва: Мир, 1984.
-
Колмогоров А.Н. Математика в ее историческом развитии. М.: Наука, 1991.
-
Harmony of spheres. The Oxford dictionary of philosophy, Oxford University Press, 1994, 1996, 2005.
-
Dimitrov Vladimir. A new kind of social science. Study of self-organization of human dynamics. Morrisville Lulu Press, 2005.
-
Herz-Fischler, Roger. A Mathematical History of the Golden Number. New York: Dover Publications, Inc., 1998.
-
Петухов С.В. Матричная генетика, алгебры генетического кода, помехоустойчивость. Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008.
-
Лосев А. История философии как школа мысли. Коммунист, 1981, №1.
-
Веннинджер М. Модели многогранников. Пер. с англ. М.: Мир, 1974.
-
Stakhov A.P. The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М.: Наука, 1989.
-
Гика Матила. Эстетика пропорций в природе и искусстве (пер. с фр.). Москва: Издательство Академии Архитектуры , 1936.
-
Гримм Г.Д. Пропорциональность в архитектуре. Ленинград-Москва: ОНТИ, 1935.
-
Gardner Martin. Mathematics, Magic and Mystery. New York: Publishing House “Dover”, 1952.
-
Пойа Д. Математическое открытие (перевод с англ.). М.: Наука, 1970. (английское издание, том 1, 1962, том 2, 1965)
-
Митропольский Ю.А. Отзыв о научном направлении украинского ученого, доктора технических наук, профессора Алексея Петровича Стахова // «Академия Тринитаризма», М., Эл № 77-6567,публ.12452, 23.09.2005 http://www.trinitas.ru/rus/doc/0232/006a/02320005.htm
-
Vera W. de Spinadel. From the Golden Mean to Chaos. Nueva Libreria, 1998 (second edition, Nobuko, 2004).
-
Gazale Midhat J. Gnomon. From Pharaohs to Fractals. Princeton, New Jersey: Princeton University Press, 1999 (Русский перевод: Мидхат Газале. Гномон. От фараонов до фракталов. Москва-Ижевск: Институт компьютерных исследований, 2002.)
-
Татаренко А.А. Золотые Tm – гармонии и Dm – фракталы — суть солитоно-подобного Тm – cтруктурогенеза мира // «Академия Тринитаризма», М., Эл № 77-6567, публ.12691, 09.12.2005
-
Аракелян Грант. Числа и величины в современной физике. Ереван: Изд. АН, 1989.
-
Шенягин В.П. «Пифагор, или Каждый создает свой миф» - четырнадцать лет с момента первой публикации о квадратичных мантиссовых s-пропорциях // «Академия Тринитаризма», М., Эл № 77-6567, публ.17031, 27.11.2011
-
Falcon Sergio, Plaza Angel. On the Fibonacci k-numbers Chaos, Solitons & Fractals, Volume 32, Issue 5, June 2007 : 1615-1624.
-
A.P. Stakhov, On the general theory of hyperbolic functions based on the hyperbolic Fibonacci and Lucas functions and on Hilbert’s Fourth Problem. Visual Mathematics, Vol. 15, No.1, 2013. http://www.mi.sanu.ac.rs/vismath/2013stakhov/hyp.pdf
-
A. Stakhov, S. Aranson, “Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem.” Applied Mathematics, 2011, No.1 (January), No.2 (February), No.3 (March).
-
Стахов, А.П. Формулы Газале, новый класс гиперболических функций Фибоначчи и Люка и усовершенствованный метод «золотой» криптографии // «Академия Тринитаризма», М.,Эл № 77-6567, публ.14098, 21.12.2006
-
Стахов А.П., Теория λ -чисел Фибоначчи // «Академия Тринитаризма», М., Эл № 77-6567, публ.17407, 05.04.2012 http://www.trinitas.ru/rus/doc/0232/009a/02321250.htm
-
А.П. Стахов, Математизация гармонии и гармонизация математики // «Академия Тринитаризма», М., Эл № 77-6567, публ.16897, 16.10.2011 http://www.trinitas.ru/rus/doc/0232/100a/02320066.htm
-
Fullerene. From Wikipedia, the free encyclopaedia http://en.wikipedia.org/wiki/Fullerene
-
Quasicrystal. http://en.wikipedia.org/wiki/Quasicrystal
-
G. Bergman, A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98-119.
-
A.P. Stakhov, “The Golden Section in the Measurement Theory,” Computers & Mathematics with Applications, 1989, Vol. 17, No 4-6, 613-638.
-
A.P. Stakhov, “Generalized golden sections and a new approach to geometric definition of a number. Ukrainian Mathematical Journal, vol. 56, 2004:-1143 – 1150 (Russian).
-
A.P. Stakhov, “Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic” // The Computer Journal, 2002, Vol. 45, No. 2, 221-236.
-
A.P. Stakhov, “A generalization of the Fibonacci Q-matrix” // Reports of the National Academy of Sciences of Ukraine, 1999, No 9, 46-49.
-
Stakhov A. “Fibonacci matrices, a generalization of the “Cassini formula,” and a new coding theory” // Chaos, Solitons & Fractals, 2006, Vol. 30, Issue 1, 56-66. http://www.trinitas.ru/rus/doc/0232/004a/02321039.htm
-
A.P. Stakhov, The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
. Stakhov, “The “golden” matrices and a new kind of cryptography.” Chaos, Solitons & Fractals 2007, Volume 32, Issue 3, 1138-1146.
-
A. Stakhov, S. Aranson. “Golden” Fibonacci Goniometry. Fibonacci-Lorentz Transformations, and Hilbert’s Fourth Problem. Congressus Numerantium, 193 (2008), 119-156.
-
A.P. Stakhov, “The Golden Section and Modern Harmony Mathematics.” Applications of Fibonacci Numbers, Kluwer Academic Publishing, Volume 7, 1998: 393-399.
-
Стахов А. П., Ткаченко И. С. Гиперболическая тригонометрия Фибоначчи // Доклады Академии наук УССР, том 208, № 7, 1993.
-
Stakhov A., Rozin B. On a new class of hyperbolic function // Chaos, Solitons & Fractals, 2005, Vol. 23, Issue 2, 379-389.
-
Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. // Украинский математический журнал, 2004, Vol. 56, No. 8, 1143-1150.
Последние публикации:
Георгий Васильевич Чефранов в моей жизни –
(01/10/2013)
Тайны науки, гипотеза вечно колеблющейся Вселенной и космическое религиозное чувство Альберта Эйнштейна –
(25/09/2013)
Лики божественной гармонии. Часть 4. –
(23/09/2013)
Лики божественной гармонии. Часть 2. –
(19/09/2013)
Лики божественной гармонии. Часть 1. –
(18/09/2013)
Необходимо зарегистрироваться, чтобы иметь возможность оставлять комментарии и подписываться на материалы