Аннотация
Выдающийся русский философ Алексей Лосев, исследователь эстетики античности и эпохи Возрождения, в следующих словах сформулировал «золотую» парадигму древних греков: «С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения». Новейшие открытия современной науки, основанные на Платоновых телах, золотом сечении, числах Фибоначчи: фуллерены, Нобелевская Премия – 1996; квазикристаллы, Нобелевская Премия – 2011; экспериментальное доказательство существования гармонии «золотого сечения» в квантовом мире; обнаружение фибоначчиевой закономерности в таблице Менделеева; «гипотеза Прокла» и новый взгляд на «Начала» Евклида и историю развития математики, начиная с Евклида; гиперболические фунции Фибоначчи и новая геометрическая теория филлотаксиса; треугольник Паскаля и обобщенные числа Фибоначчи; обобщенные золотые пропорции и закон структурной гармонии систем; лямбда-числа Фибоначчи как новый класс целочисленных последовательностей, обладающих уникальными математическими свойствами; «металлические пропорции» и общая теория гармонических гиперболических функций; решение четвертой проблемы Гильберта и поиск гармонических гиперболических миров Природы; "золотые" матрицы, преобразования Фибоначчи-Лоренца и «золотая» интерпретация специальной теории относительности; «золотые» геноматрицы; алгоритмическая теории измерений, коды и компьютеры Фибоначчи; системы счисления с иррациональными основаниями, троичная зеркально-симметричная арифметика и "золотая" теория чисел как новое направление в теории чисел; обобщенные матрицы Фибоначчи и новая теория кодирования; наконец, «математика гармонии» как новое междисциплинарное направление, восходящее к «Началам» Евклида, - все это «лики божественной гармонии» в современной науке, которые создают общую картину ее движения к "Золотой" Научной Революции, что в совокупности отражает одну из важнейших тенденций в развитии современной науки – возврат к Пифагору, Платону и Евклиду.
Часть I
«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».
Бертран Рассел
Предисловие
Каждому из нас не раз приходилось задумываться над тем, почему Природа способна создавать такие удивительные эстетические структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие? В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Что такое «гармония»? И имеет ли она математическое выражение? Для моделирования «мира гармонии» в античном мире, прежде всего в Древней Греции, была создана математика гармонии, элементы которой возрождены в современной науке во многих книгах [1 - 25], включая книгу Alexey Stakhov “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science”, опубликованной в 2009 г. одним из наиболее престижных научных издательств мира “World Scientific” [25].
Цель настоящей публикации, предназначенной для широкой аудитории, состоит в том, чтобы популярно объяснить понятие «гармонии», которое было введено в науку на заре развития человеческой цивилизации, рассказать об истории этого направления в античный период, эпоху средневековья, эпоху Возрождения, в 19 и 20 веках, а также ввести в круг идей и приложений современной «математики гармонии», автивно развивающейся в 21 в. [25]. Конечно, «математика гармонии» - это раздел математики; поэтому полностю избежать математических формул в статье, посвященной этой математической дисциплине, авторам не удалось. Однако, «математика гармонии» - это достаточно простая (можно сказать, «элементарная») математика, в которой используются математические формулы, доступные школьникам старших классов. И авторы надеются на снисхождение наших читателей.
Статья состоит из 4-х частей:
Часть I. Золотое сечение и «пентакл Венеры»
Часть II. Числа Фибоначчи и 10-я проблема Гильберта
Часть III. Платоновы тела, «гипотеза Прокла», новый взгляд на «Начала» Евклида, фуллерены и квазикристаллы
Часть IV. Роль «математики гармонии» в развитии современной науки
Часть I. Золотое сечение и «пентакл Венеры»
1. Понятие «гармонии» в своем историческом развитии
В поисках истоков гармонии
Гармония, как фундаментальное условие жизни Вселенной, существовала задолго до появления человека. Чтобы убедиться в этом, достаточно лишь внимательно присмотреться к окружающему нас миру и его устройству: синхронным движениям планет, филлотаксису, пентагональной симметрии, форме кристаллов, молекул и ДНК. Человек всегда обладал той или иной способностью улавливать «музыку сфер», он ею вдохновлялся и переносил в земные творения - прежде всего в музыку и архитектуру. Поэты и композиторы, художники и скульпторы, настроившись на гармонические вибрации, сумели передать в своих работах те самые законы и пропорции, которые лежат в основе Вселенной.
Современные ученые в попытках понять порядок и устройство мироздания накопили огромное количество информации, основали бесчисленные научные направления и традиции, неустанно изобретают сложные теории и формулы, ежегодно публикуют десятки тысяч научных статей, но все меньше способны видеть целое. Ведь чем больше фрагментировано и разрознено знание, тем сложнее видеть взаимосвязи и единство, отказаться от привычных схем и увидеть мир целиком, как это делали мудрецы древности.
Мы уверены, что если современные учёные сумеют подняться над собственным эгоизмом и клановым соперничеством, если будут действовать, понимая суть гармонии и помнить об её истоках, то мир станет немного лучше. Именно поэтому очень важно выяснить, где и когда появился первый источник знаний о «гармонии», который со временем превратился в научное наследие цивилизации. Начнем с того, что приведем цитаты из трудов некоторых известных в научном мире людей. Что же подразумевалось под понятием «гармония» в различные исторические эпохи?
Пифагор, посвящённый в египетские мистерии, впервые применил термин «гармония» для обозначения Мира. Пифагорейцы следовали идее о гармонической конструкции Мироздания, а сама гармония для них имела численное выражение, то есть, была интегрально связана с концепцией числа. Согласно пифагорейцам, «гармония представляет собою внутреннюю связь вещей, без которой космос не смог бы существовать». Наконец, согласно Пифагору, гармония имеет численное выражение, то есть, она интегрально связана с концепцией числа. Пифагорейцы создали учение о созидательной сущности числа. Аристотель в «Метафизике» отмечет именно эту особенность пифагорейского учения:
«Так называемые пифагорейцы, занявшись математическим науками, впервые двинули их вперед и, воспитавшись на них, стали считать их началами всех вещей ... Так как, следовательно, всё остальное явным образом уподоблялось числам по всему своему существу, а числа занимали первое место во всей природе, элементы чисел они предположили элементами всех вещей и всю вселенную [признали] гармонией и числом».
Платон. Пифагорейское учение о числовой гармонии мироздания имело огромную созидательную силу и оказало большое влияние на развитие всех последующих учений о природе и сущности гармонии, в частности, оно лежит в основе Космологии Платона. В своих работах Платон развивает пифагорейское учение, особенно подчеркивая космическое значение гармонии. Он твердо убежден в том, что мировую гармонию можно выразить в числовых пропорциях. Влияние пифагорейцев особенно прослеживается в «Тимее», где Платон вслед за пифагорейцами развивает учение о пропорциях и анализирует роль правильных многогранников («Платоновых тел»), из которых, по его мнению, Бог создал мир.
Гераклит Диалектическое понимание гармонии было сформулировано знаменитым греческим философом Гераклитом. У древнего мыслителя мир, то есть Космос, совершенен, гармоничен и потому «божественен». В гераклитовском понимании гармония — это внутреннее единство, согласованность, уравновешенность противоположностей, составляющих целое. «Расходящееся сходится, а из различного образуется прекраснейшая гармония, и все возникает через противопоставление».
В эстетике Гераклита на первом месте стоит онтологическое понимание гармонии, гармония присуща, прежде всего, объективному миру вещей, самому космосу. Она присуща и природе искусства. Характерно, что, когда Гераклит хочет наиболее наглядно раскрыть природу гармонии, он обращается к искусству. Лучше всего гармонию космоса иллюстрирует у Гераклита образ лиры, в которой различно натянутые струны создают великолепное звучание. Категория гармонии обладает у Гераклита не только онтологическим, но и ценностным значением, в ней присутствует момент оценки. Особенно ярко это выражается в учении о двух видах гармонии: «скрытой» и «явной». Наиболее содержательной является скрытая, или непроявленная гармония. Гераклит утверждает: «Скрытая гармония сильнее явной».
Главный вывод, который вытекает из учений Пифагора, Гераклита и Платона, состоит в том, что гармония объективна, она существует независимо от нашего сознания и выражается в гармоничном устройстве всего сущего, начиная с космоса, и заканчивая микромиром. Но если Гармония объективна, то она должна стать предметом математического исследования. Эта идея и лежит в основе «математики гармонии» [25].
Иоганн Кеплер. Неоценимый вклад в развитие учения о гармонии внес Иоганн Кеплер. Его книга «Harmonies Mundi» («Гармония мира») занимает особое место в истории науки не только потому, что содержит формулировку третьего закона Кеплера, но также и потому, что это одна из первых книг, посвященных гармонии Космоса. Из своего открытия (третий закон Кеплера) он делает следующий вывод, имееющий прямое отношение к гармонии Солнечной системы («музыка сфер»): «Таким образом, небесные движения суть не что иное, как ни на миг не прекращающаяся многоголосая музыка (воспринимаемая не слухом, но разумом)».
Русский биограф Кеплера Е.А. Предтеченский (1860 - 1904) пишет:
«Царящая в мире чудная гармония понималась Кеплером не в отвлеченном только смысле благоустройства, а звучала в его поэтической душе настоящей музыкой, которую мы могли бы понять не иначе, как совершенно войдя в круг его идей и проникшись его могучим энтузиазмом к дивному устройству мира и пифагорейским благоговением перед числовыми отношениями. В самом деле, разве не удивительно, что «прекрасное» для слуха зависит от строгого численного соотношения, например, между длинами струн, производящих звуки, — соотношения, открытого Пифагором? Но в Кеплере, несомненно, обитала часть души Пифагора, и мудрено ли, что он усматривал числовые соотношения в открытом и объясненном им планетном космосе?»
Леон-Баттиста Альберти Известный итальянский теоретик архитектуры Леон-Баттиста Альберти, написавший много книг о зодчестве, говорил о гармонии следующее (цит. по [24]):
«Есть нечто большее, слагающееся из сочетания и связи трех вещей (числа, ограничения и размещения), нечто, чем чудесно озаряется весь лик красоты. Это мы называем гармонией, которая, без сомнения, источник всякой прелести и красоты. Ведь назначение и цель гармонии – упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту… Она охватывает всю жизнь человеческую, пронизывает всю природу вещей. Ибо все, что производит природа, все это соизмеряется законом гармонии. И нет у природы большей заботы, чем та, чтобы произведенное ею было совершенным. Этого никак не достичь без гармонии, ибо без нее распадается высшее согласие частей».
В.П. Шестаков. Известный советский философ В.П. Шестаков в книге [26] выделяет, по крайней мере, три типа понимания гармонии: математическое, эстетическое и художественное. В математическом смысле гармония понимается как равенство или соразмерность частей друг с другом и части с целым. При этом, как подчеркивает Шестаков, «математическое понимание гармонии фиксирует, прежде всего, количественную определенность гармонии, но оно не заключает в себе представления об эстетическом качестве гармонии, ее выразительности, связи с красотой». Он обращает внимание на одну важную особенность определения гармонии, данного Альберти: «Гармония является законом не только искусства, но и природы, она охватывает всю жизнь человека и всю природу вещей. Гармония в искусстве является отражением гармонии в природе». Заметим, что изучение количественных или математических аспектов «гармонии» и является главной задачей «математики гармонии» [25].
Иосиф Шевелев. Существуют различные понимания гармонии, выражающие ее через другие фундаментальные понятия, в частности, через понятие целостности. Эта идея развита в книге «Метаязык живой природы» [15], написанной Иосифом Шевелевым, известным российским архитектором и исследователем гармонии. Шевелев утверждает:
«Понятие целостность, хорошо известное... как категория, размытая во многих других философских понятиях, таких, как единое и единство, форма и содержание, материя и сознание, вещество, пространство и время, гармония и Бог. Современное естествознание применяет его нередко, но не как понятие науки, ясно определенное, а, скорее, как символ и образ. Закона целостности наука не устанавливает... Если закон целостности действительно существует, то в силу того, что охватывается этим законом, он оказывается вне сферы науки. Он не может быть производным от физической реальности. Он может существовать только как априорная данность, не имеющая истока в феноменальном мире; как идея связи всего со всем, реализуемая всеми материальными структурами живой природы на всех иерархических уровнях их внутренней организации».
Тейяр де Шарден. Французский философ Тейяр де Шарден в своей книге «Феномен человека» [27] утверждает:
«Согласованность частей Универсума всегда была предметом восхищения людей. И эта согласованность, по мере того, как наука все более точно и глубоко изучает факты, оказывается все более удивительной. Каждый элемент космоса буквально соткан из всех других элементов. Снизу он создан таинственным явлением композиции, сверху – воздействием единства высшего порядка. ...Универсум держится своей совокупностью. Существует лишь один возможный способ рассматривать его – это брать его как блок, весь целиком».
Эдуард Сороко. Современный белорусский философ Эдуард Сороко начинает свою замечательную книгу «Структурная гармония систем» [8] следующими словами:
«Если и существуют «вечные» проблемы, которые постоянно держит в поле зрения исследовательская мысль, то среди них в первую очередь можно назвать проблему гармонии. Наука, физика в частности, по словам Б.Г.Кузнецова, всегда имела своей извечной фундаментальной целью «найти в лабиринте наблюдаемых фактов объективную гармонию»... То же можно сказать в адрес философии, искусства (живописи, музыки, архитектуры) и других областей самореализации «человеческого духа».
Дарио Салас Соммэр. Самым первым источником знаний о «гармонии» считается Герметическая Философия, самая древняя из всех известных систем знания. Считается, что впервые представление о мире как о гармоническом целом, берущим начало от Единого Бога, было развито в науке Древнего Египта Гермесом Трисмегистом, и уже затем это понятие закрепилось в древнегреческой традиции, где Гармония представлена как организация Вселенной, как Космос, противоположный Хаосу.
Многочисленные публикации и интернет-статьи на тему герметизма в основном связаны с вульгарным оккультизмом, спиритизмом и эзотерикой. Стоило большого труда отыскать нечто стоящее в этом океане вымысла и фантазий. Работы Дарио Саласа Соммэра, философа из Чили [28 - 31], привлекают своей простотой и ясностью, они наполнены идеалом служения человечеству, искренним желанием помочь обрести правильный путь через реальные практические знания. Именно наличие практической составляющей отличает философию герметизма от других теоретических дисциплин. Все это послужило критерием доверия к тому, о чём пишет этот интересный учёный
В одной из своих статей [30] Дарио Салас обращает внимание на связь герметической философии с «математикой гармонии» [25]:
«Золотая Математика и Герметическая Философия могут стать незыблемым фундаментом, поясняющим жизненную необходимость гармоничного существования людей, и разработать критерии «золотого поведения человека». Мы могли бы обосновать необходимость для государств инвестировать в развитие Морали и Сознания, чтобы все понимали Мораль как совокупность законов Природы, при выполнении которых жизнь будет наполненной и успешной в духовном и материальном плане. И тогда, со временем, появятся мудрые лидеры, которые будут обладать высшим сознанием, а не просто энциклопедическими знаниями; лидеры, имеющие духовные ценности и высшую Мораль, внутреннюю целостность и широкое видение реальности».
По мнению Дарио Саласа Соммэра, "...гармония - это музыка, ритм и пульс космического оркестра, которым дирижирует сам Создатель..."
2. Математизация гармонии
Математическое учение о Природе древних греков
Согласно мнению выдающегося американского историка математики Мориса Клайна [32], главный вклад древних греков, «оказавший решающее влияние на всю последующую культуру, состоял в том, что они взялись за изучение законов природы». Основной вывод, вытекающий из книги Мориса Клайна [32], состоит в том, что древние греки предложили новаторскую концепцию космоса, в котором все было подчинено математическим законам. Возникает вопрос: когда эта концепция была разработана? Ответ на этот вопрос также содержится в книге [32]:
«Греки преисполнились решимости доискаться до истин и, в частности, до истин о математических основах природы. Как следует приступить к поиску истин и как при этом гарантировать, что поиск действительно приводит к истинам? Греки предложили «план» такого поиска. Хотя он создавался постепенно на протяжении нескольких веков (VI-III вв. до н.э.), в истории науки расходятся во мнении относительно того, когда и кем этот план был впервые задуман, к III в. до н.э. план поиска истин был доведен до совершенства».
Таким образом, по мнению Клайна, новаторская концепция космоса, основанного на математических законах, была разработана древними греками в период с VI до III вв. до н.э. Но согласно утверждению А.Н. Колмогорова [33], в этот же период в Древней Греции «возникает математика как самостоятельная наука с ясным пониманием своеобразия ее метода и необходимости систематического развития ее основных понятий и предложений в достаточно общей форме».
Но тогда возникает вопрос: существовала ли какая-либо взаимосвязь между процессом создания математического учения о природе, что считается главным достижением древнегреческой науки [32], и процессом создания математики [33], которые протекали в Древней Греции в один и тот же период. Или это разные процессы? Оказывается, что такая связь, безусловно, существовала. Более того. Можно утверждать, что эти процессы фактически совпадали, то есть, математика, созданная древними греками, и их учение о природе, основанное на математических принципах, - это одно и то же. И наиболее ярким воплощением процесса «Математизации Гармонии» являются «Начала» Евклида, написанные в III в. до н.э.
Введение термина «математика гармонии»
В конце 20 в. для обозначения математического учения о природе, созданного древними греками, был введен термин “the mathematics of harmony” (математика гармонии). Следует отметить, что этот термин выбран очень удачно, потому что он отражал главную идею античной науки – «Математизация Гармонии». Впервые этот термин был введен в небольшой статье “Harmony of spheres”, помещенной в «The Oxford dictionary of philosophy» [34]. В этой статье понятие “the mathematics of harmony” («математика гармонии») ассоциируется с «гармонией сфер», которая называлась также «гармонией мира» (harmonica mundi) или мировой музыкой (лат. musica mundana). Гармония сфер представляет собой античное и средневековое учение о музыкально-математическом устройстве космоса, восходящее к
пифагорейской и
платонической философской традиции.
Еще одно упоминание о «математике гармонии» применительно к древнегреческой математике мы встречаем в книге [35]. Важно подчеркнуть, что в книге [35] понятие “the mathematics of harmony” («математика гармонии») непосредственно ассоциируется с «золотым сечением» - важнейшим математическим открытием античной науки в области гармонии, которое в тот период называлось «делением отрезка в крайнем и среднем отношении».
3. Золотое сечение: алгебраические и геометрические свойства
Геометрическое определение
Как известно, количество иррациональных (или несоизмеримых) чисел бесконечно. Однако, некоторые из них занимают особое место в истории математики, более того – в истории материальной и духовной культуры человечества. Их значение состоит в том, что они выражают некоторые отношения, имеющие универсальный характер и обнаруживающиеся в самых неожиданных местах.
Первое из них – это иррациональное число
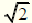
, равное отношению диагонали к стороне квадрата. С этим числом связано открытие несоизмеримых отрезков и история наиболее драматичного периода в античной математике, который привел к разработке теории иррациональностей и иррациональных чисел и в конечном итоге – к созданию современной «непрерывной» математики.
Следующие два ирациональных числа – это число , выражающее отношение длины окружности к ее диаметру, и «неперово» число
е, основание «натуральных логарифмов». Как известно, число
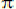
лежит в основе тригонометрических функций и тригонометрии, а число
е лежит в основе так называемых гиперболических функций, которые были использованы Николаем Лобачевским при описании математических соотношений созданной им «гиперболической геометрии», которая считается наиболее крупным математическим открытием 19 в.
Еще одно знаменитое иррациональное число – это «золотое сечение» или «золотая пропорция»

(1)
Это число возникает как результат решения геометрической «задачи о делении отрезка в крайнем и среднем отношении» (Рис.1).
Рис.1. Деление отрезка в крайнем и среднем отношении («золотое сечение»)
Эта задача описана в «Началах» Евклида. Ее суть состоит в том, чтобы разделить отрезок АВ точкой С в такой пропорции, чтобы большая часть отрезка СВ так относилась к меньшей части АС, как отрезок АВ к своей большей части СВ (Рис. 1), то есть:
AB:CB=CB:AC (2)
Решая пропорцию (2), мы приходим к следующему алгебраическому уравнение для вычисления искомого отношения x:
x2-x-1=0. (3)
Из «физического смысла» пропорции (3) (отношение большего к меньшему) вытекает, что искомое решение уравнения (3) должно быть положительным числом, откуда вытекает, что решением «задачи о делении отрезка в крайнем и среднем отношении» является положительный корень уравнения (3), который выражается формулой (1).
Выведенное выше алгебраическое уравнение (3) часто называют уравнением золотой пропорции.
Происхождение термина «золотое сечение»
Именно «золотое сечение», обладающее уникальными алгебраическими и геометрическими свойствами, стало эстетическим каноном древнегреческого искусства и искусства эпохи Возрождения. Об этом мы расскажем ниже.
Кто же ввел термин «Золотое Сечение»? Иногда введение этого названия (“section aurea”) приписывают Леонардо да Винчи. Однако, это – спорное утверждение, потому что название «золотое сечение» не встречается в сочинених Леонардо да Винчи. В книге [36], посвященной истории «золотого числа», утверждается, что впервые ввел термин «золотое сечение» (“Goldene Shnitt”) немецкий математик Мартин Ом в 1835 г. в книге “Die reine Elementar-Mathematik”.
Обозначение «золотой пропорции» греческой буквой Ф (число
PHI) не является случайным. Эта буква является первой буквой в имени знаменитого греческого скульптора Фидия (
греч. Φειδίας), который широко использовал «золотое сечение» в своих скульптурных произведениях. Напомним, что Фидий (5 в. до н.э.) наряду с Поликлетом являлся одним из двух самых значительных и авторитетных мастеров древнегреческой скульптуры эпохи классики. Он прославился тем, что руководил работами по художественному убранству Акрополя, исполнив колоссальную бронзовую статую Афины Промахос («Победительницы в битвах»), воздвигнутую здесь около 456 до н.э. в ознаменование победы греков над персами. Создал также две грандиозные (из золота и слоновой кости) статуи: Афины Парфенос («Девы») для Парфенона на Акрополе (446–438 до н.э.) и Зевса Олимпийского (для храма Зевса в Олимпии, ок. 430 до н.э.), которого считали одним из «семи чудес света». При всей монументальности его образов, порой (подобно 9-метровой Афине Парфенос или 13-метровому Зевсу Олимпийскому) беспрецедентных по величине для Греции того времени, им была свойственна строгая уравновешенность и гармония пластических контрастов, основанная на золотом сечении, что и составляло суть классического стиля в период его высшего расцвета.
Алгебраические свойства «золотой пропорции»
Начнем с установления простейших алгебраических свойств золотой пропорции. Для этого представим уравнение (3) в следующем виде:
x2=x+1. (4)
Если корень Ф (золотая пропорция) подставить вместо x в уравнение (4), то мы получим следующее замечательное тождество для золотой пропорции:
Ф2= Ф+1. (5)
Если все члены тождества (5) разделить на Ф, то мы придем к следующему выражению для F:
Ф=1+1/ Ф, (6)
которое может быть представлено и в следующем виде:
Ф-1=1/ Ф. (7)
Проанализируем тождество (7). Известно, что любое действительное число а имеет обратное к нему число 1/а. Например, дробь 0,1 является числом, обратным к 10. Традиционный алгоритм получения обратного числа 1/а из исходного числа а состоит в делении числа 1 на число а. Это довольно сложная процедура. Попробуйте, например, путем деления получить число, обратное к а = 357821 . Это можно сделать только с помощью современного компьютера.
Рассмотрим теперь золотую пропорцию (1). Как получить из нее обратное ей число 1/ Ф? Тождество (7) дает очень простой ответ на этот вопрос. Для этого достаточно вычесть единицу из золотой пропорции F. И константа Ф - единственное число, которое обладает таким свойством!
Если теперь многократно умножать (и делить) члены выражения (5) на Ф и устремить этот процесс до бесконечности, то мы придем к следующему изящному тождеству, связывающему степени золотой пропорции:
Фn=Фn-1+Фn-2; n=0,±1,±2,±3,… (8)
Тождество (8) словесно можно выразить следующим образом: «Любая целая степень золотой пропорции равна сумме двух предыдущих».
Представление «золотой пропорции» в радикалах
Рассмотрим теперь еще раз тождество (5). Если взять корень квадратный из правой и левой частей тождества (5), то получим следующее выражение для Ф:
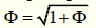
(9)
Если теперь в правой части выражения (9) вместо Ф подставить его же выражение, задаваемое (9), то получим следующее удивительное представление золотой пропорции в «радикалах»:
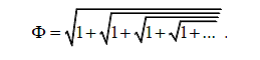
. (10)
Представление «золотой пропорции» в виде цепной дроби
Представим теперь «золотое сечение» Ф в виде цепной дроби. Для этого воспользуемся тождеством (6). Если в правую часть тождества (6) вместо Ф подставить его значение, задаваемое тем же выражением (6) и продолжить этот процесс до бесконечности, то мы придем еще к одному представлению Ф в виде следующей «многоэтажной» дроби с бесконечным количеством «этажей»:
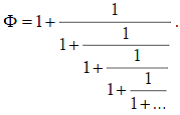
. (11)
Оказывается, что выражение (11) имеет глубокий математический смысл. В работах российских математиков А.Я. Хинчина и Н.Н. Воробьева обращено внимание на тот факт, что выражение (11) выделяет золотую пропорцию Ф среди других иррациональных чисел, так как согласно (11) золотая пропорция наиболее медленно апроксимируется рациональными дробями. Это означает, что, с точки зрения цепных дробей, золотая пропорция является уникальным иррациональным числом.
И в заключение несколько слов об эстетической стороне полученных выше алгебраических свойств «золотой пропорции», задаваемых выражениями (8), (10), (11). Каждый математик интуитивно стремится представить свои математические результаты в наиболее простой, компактной форме. И если такую форму удается найти, то это доставляет математику «эстетическое наслаждение». В этом и состоит эстетическая ценность многих математических формул! В этом отношении (стремление к «эстетическому» выражению математических результатов) математическое творчество подобно творчеству композитора или поэта, главной задачей которых является получение совершенных музыкальных или поэтических форм, доставляющих «эстетическое удовольствие». Заметим, что представления золотой пропорции в виде (10), (11) доставляют нам «эстетическое наслаждение» и вызывают неосознанное чувство ритма и гармонии, когда мы начинаем задумываться над бесконечной повторяемостью одних и тех же простых математических элементов в выражениях для Ф, задаваемых (10), (11).
«Принцип математической красоты» Дирака
В настоящее время ни у кого не вызывает сомнения, что «наука прекрасна, ибо она отражает в себе и преломляет в нашем сознании красоту, гармонию и единство мироздания» [24]. Но физики пошли еще дальше. Английский физик Нобелевский Лауреат Поль Дирак выдвинул тезис: «Красота является критерием истинности физической теории». Дирак не только осознавал красоту выражений математических формулировок теории, но и понимал эвристическую, регулятивную роль красоты как методологического принципа построения научного знания. Дирак пишет (цитата взята из [24]):
"Я чувствую, что теория, если она правильна, должна быть красивой (beautiful), так как мы руководствуемся принципом красоты, когда устанавливаем фундаментальные законы. Так, в исследованиях, опирающихся на математику, мы часто руководствуемся требованием математической красоты. Если уравнения физики некрасивы с математической точки зрения, то это означает, что они несовершенны и что теория ущербна и нуждается в улучшении. Бывают случаи, когда математической красоте должно отдаваться предпочтение (по крайней мере, временно) перед согласием с экспериментом. Дело обстоит так, будто Бог создал Вселенную на основе прекрасной математики и мы сочли разумным предположение, что основные идеи должны выражаться в терминах прекрасной математики".
Это замечательное высказывание Дирака является путеводной нитью для «математики гармонии» [25], которая ставит своей задачей поиск совершенных пропорций, которые в «скрытом» виде выражают «гармонию» многих явлений окружающей нас Природы.
Геометрические свойства «золотого сечения»
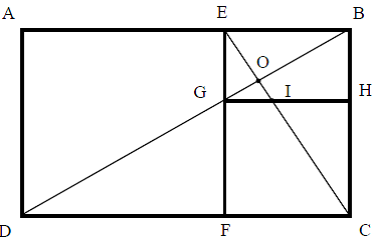
Золотой прямоугольник. Мы начнем наше путешествие по геометрическим свойствам золотого сечения с «золотого» прямоугольника (Рис.2), под которым понимается прямоугольник, в котором отношение большей стороны к меньшей равно золотой пропорции, то есть,
Рис.2. «Золотой» прямоугольник
Рассмотрим случай, когда
AB = Ф и
BC= 1 . Найдем на отрезках
AB и
DC точки
E и
F , которые делят соответствующие стороны
AB и
DC в «золотом сечении». Ясно, что
AE=DF=1, тогда
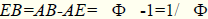
.
Соединим теперь точки E и F отрезком EF и назовем его «золотой линией». При этом с помощью золотой линии EF золотой прямоугольник ABCD оказывается разделенным на два прямоугольника AEFD и EBCF. Поскольку все стороны прямоугольника AEFD равны между собой, то этот прямоугольник есть ни что иное, как квадрат.
Рассмотрим теперь прямоугольник EBCF. Поскольку его большая сторона BC=1, а меньшая EB=1/Ф, то отсюда следует, что их отношение BC:EB= Ф и, следовательно, прямоугольник EBCF также является «золотым»! Таким образом, золотая линия EF расчленяет исходный «золотой» прямоугольник ABCD на квадрат AEFD и новый золотой прямоугольник EBCF.
Повторяя многократно эту процедуру, мы получим бесконечную последовательность квадратов и «золотых» прямоугольников, которые в пределе сходятся в точке O.
Заметим, что такое бесконечное повторение одних и тех же геометрических фигур, то есть, квадрата и «золотого» прямоугольника, вызывает у нас неосознанное эстетическое чувство ритма и гармонии. Считается, что именно это обстоятельство является причиной того, что многие предметы прямоугольной формы, с которыми человек имеет дело (спичечные коробки, зажигалки, книги, чемоданы), зачастую имеют форму «золотого» прямоугольника (см. примеры ниже).
Рис.3. Прямоугольные предметы, имеющие форму «золотого» прямоугольника
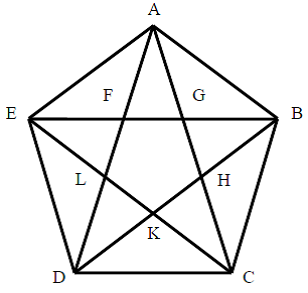
Пентагон и пентаграмма. Существуют еще ряд замечательных геометрических фигур, основанных на золотом сечении. «Золотое сечение» лежит в основе правильного пятиугольника, называемого также «пентагоном» (Рис.4). Слово «пентагон» происходит от греческого слова «pentagonon» – пятиугольник.
Рис.4. Пентагон и пентаграмма
Если в пентагоне провести все диагонали, то в результате мы получим хорошо известную нам пятиугольную звезду, называемую также пентаграммой или пентаклом. Название «пентаграмма» происходит от греческого слова «pentagrammon» (pente – пять и grammon – линия) и означает правильный пятиугольник, на сторонах которого построены равнобедренные треугольники одинаковой высоты. Доказано, что точки пересечения диагоналей в пентагоне всегда являются точками золотого сечения. При этом они образуют новый пентагон FGHKL. В новом пентагоне можно провести диагонали, пересечение которых образуют еще один пентагон и это процесс может быть продолжен до бесконечности. Таким образом, пентагон ABCDE как бы состоит из бесконечного числа пентагонов, которые каждый раз образуются точками пересечения диагоналей. Эта бесконечная повторяемость одной и той же геометрической фигуры создает чувство ритма и гармонии, которое неосознанно фиксируется нашим разумом.
Пентаграмма вызывала особое восхищение у пифагорейцев и считалась их главным опознавательным знаком. Существует следующая легенда. Когда на чужбине один из пифагорейцев лежал на смертном одре и не мог заплатить человеку, который за ним ухаживал, то он велел ему изобразить на своем жилище пентаграмму, надеясь на то, что этот знак увидит кто-либо из пифагорейцев. И действительно, несколько лет спустя, один пифагореец увидел этот знак, и хозяин дома получил богатое вознаграждение.
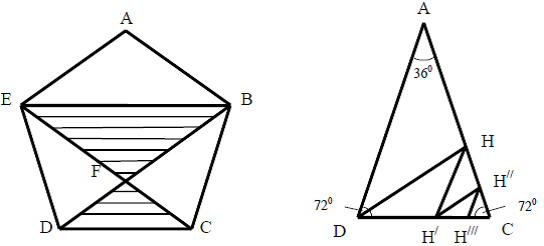
Золотая чаша и золотой равнобедренный треугольник. Пентагон и пентаграмма на Рис.4 включают в себя ряд замечательных фигур, которые широко использовались в произведениях искусства. В античном искусстве широко известен так называемый «закон золотой чаши» (Рис.5), который использовали античные скульпторы и золотых дел мастера. Заштрихованная часть пентагона на Рис.5 дает схематическое представление «золотой» чаши, котрое напоминает знаменитый советский «знак качества».
Рис.5. «Золотая» чаша Рис.6. «Золотой»
равнобедренный треугольник
Пентаграмма (Рис.4) состоит из пяти «золотых» равнобедренных треугольников (Рис.6), каждый из которых напоминает букву «А» («пять пересекающихся А»). Каждый «золотой» равнобедренный треугольник на Рис.6 имеет острый угол A=36° при вершине и два острых угла D=C=72° при основании треугольника. Основная особенность «золотого» равнобедренного треугольника состоит в том, что отношение каждого бедра AC=AD к основанию DC равно золотой пропорции Ф.
Исследуя «золотой» равнобедренный треугольник, как часть пентаграммы, пифагорейцы были восхищены, когда обнаружили, что биссектриса DH совпадает с диагональю DB пентагона (Рис.4) и делит сторону AC в точке H золотым сечением (Рис.6). При этом возникает новый «золотой» треугольник DCH. Если теперь провести биссектрису угла H к точке H1 и продолжить этот процесс до бесконечности, то мы получим бесконечную последовательность «золотых» равнобедренных треугольников. Как и в случае с «золотым» прямоугольником (Рис.3) и пентагоном (Рис.4), бесконечное возникновение одной и той же геометрической фигуры («золотого» треугольника) после проведения очередной биссектрисы вызывает эстетическое чувство ритма и гармонии.
Золотое сечение в природе
Пентагональная симметрия. В живой природе широко распространены формы, основанные на «пентагональной» симметрии (морские звезды, морские ежи, цветы). Пятилепестковыми являются цветы кувшинки, шиповника, боярышника, гвоздики, груши, черемухи, яблони, земляники и многих других цветов. Ниже на Рис.7 приведены примеры структур живой природы, основанных на «пентагональной» симметрии.
а) b)
c) d)
Рис.7. Примеры пентагональной симметрии в природе: а) китайская роза; b) яблоко в разрезе; c) морская звезда; d) кактус
Свойство наличия пяти пальцев на руке или пяти костей, или костных зачатков на органах, соответствующих руке человека и многих животных («пентадактильность»), являются дополнительным свидетельством широкого распространения пятиугольных форм в морфологии биологического и растительного мира.
Пентакл Венеры. В 2010 г. на Интернете выставлена
информация о публикации новой книги «
Harmony: a New Way Of Looking At Our World» («Гармония – новый взгляд на наш мир») (2010) [21]. Сенсационность этой информации состоит в том, что автором книги [21] является Принц Чарльз, наследник английского престола.
Принц Чарльз
В книге [21] вводится понятие «Грамматика гармонии». И главная идея книги состоит в том, что Вселенная является наиболее ярким воплощением "Грамматики гармонии". В книге [21], Принц Чарльз разделяет свое убеждение в том, что наиболее актуальные проблемы человечества коренятся в нашей дисгармонии с природой, и что мы можем решить их путем восстановления баланса с естественным порядком.
В своей книге [21] Принц Чарльз большое внимание уделяет главному символу пифагорейцев - пентаклу (Рис.4), как одному из примеров «Грамматики гармонии». В своей книге Принц Чарльз обращает внимание на «пентакл Венеры», который образуется в процессе движения Венеры на небосклоне. Как известно, каждые восемь лет планета Венера описывает абсолютно правильный пентакл по большому кругу небесной сферы (Рис.8). Древние астрономы заметили это явление и были так потрясены, что Венера и ее пентакл стали символами совершенства, красоты. Как бы отдавая дань этому явлению, древние греки устраивали Олимпийские игры каждые восемь лет. Сегодня лишь немногие знают, что современные Олимпиады следуют половинному циклу Венеры. Еще меньше людей знают о том, что пятиконечная звезда едва не стала символом Олимпийских игр, но в последний момент его модифицировали: пять остроконечных концов звезды заменили пятью кольцами, по мнению организаторов, лучше отражающими дух участия и гармонию Олимпийских игр.

Рис.8. Пентакл Венеры
К блужданиям Венеры по небосклону, основанным на «пентакле» и «золотом сечении», можно было бы отнестись, как к очередной «эзотерической сенсации», если бы не одно обстоятельство. В современной науке сделано много выдающихся открытий, подтверждающих наличие «гармонических пропорций» в огромном количестве природных явлений и объектов (пентагональная симметрия, фуллерены (Нобелевская Премия по химии-1996), квазикристаллы Дана Шехтмана (Нобелевская Премия по химии - 2011), «геометрия Боднара» (филлотаксис) [12], “золотые» геноматрицы Сергея Петухова [37], экспериментальное доказательство наличия гармонии «золотого сечения» в квантовом мире и др.). Все это наталкивает на одну и ту же мысль о неслучайности нашей Вселенной, которую высказал в своей книге Принц Чарльз.
4. Золотое сечение в древнегреческой культуре
Высказывания Алексея Лосева и Иоганна Кеплера
Какая главная идея лежала в основе древнегреческой науки? Подавляющее число исследователей сходятся в одном: идея Гармонии, связанная с «золотым сечением». Как известно, в древнегреческой философии Гармония противостояла Хаосу и означала организованность Вселенной, Космоса. Выдающийся русский философ Алексей Лосев, исследователь эстетики античности и эпохи Возрождения, так оценивает основные достижения древних греков в этой области [38]:
«Космос античным мыслителям периода зрелой классики представляется не просто некоей отвлеченной неопределенностью, (в таком случае он был бы только чистой мыслью), но совершенно живым и единораздельным телом, содержащим в себе нерушимую цельность, несмотря на бесконечные различия всех его проявлений. С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения (то есть, целое относится в нем к большей части, как большая часть к меньшей). Этому закону, кстати сказать, древние греки подчиняли и свои архитектурные сооружения. Их систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».
В этом высказывании Алексей Лосев достаточно убедительно сформулировал «золотую» парадигму античной космологии. В ее основе лежат важнейшие идеи античной науки, которые в современной науке иногда трактуются как «курьезный результат безудержной и дикой фантазии». Прежде всего – это Пифагорейская доктрина о числовой гармонии мироздания и космология Платона, основанная на Платоновых телах. Обратившись к геометрической структуре мироздания и геометрическим отношениям, выражающим гармонию (Платоновы тела и «золотое сечение»), пифагорейцы предвосхитили возникновение математического естествознания, которое начало стремительно развиваться в 20-м веке. Идея Пифагора и Платона о всеобщей гармонии мироздания оказалась бессмертной.
Таким образом, в центре созданного древними греками математического учения о природе стояла «концепция гармонии», а сама математика древних греков и была «математикой гармонии» (“the mathematics of harmony”), которая непосредственно связана с «золотым сечением» - важнейшим математическим открытием античной науки в области гармонии.
А вот еще одно широко известное высказывание, касающееся золотого сечения. Оно принадлежит гениальному астроному Иоганну Кеплеру, автору трех знаменитых «Законов Кеплера». Свое восхищение золотым сечением Кеплер выразил в следующих словах:
«В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем».
Некоторые математики считают сравнение «золотого сечения» с «теоремой Пифагора» слишком большим преувеличением роли «золотого сечения» в математике. Этим математикам не следует забывать, что Иоганн Кеплер был не только гениальным астрономом, но и гениальным математиком, чего не всегда можно сказать о математиках, которые его критикуют.
Примеры памятников древнегреческой культуры
Достаточно детально приложения «золотого сечения» в античной культуре описаны в книге [19]. Приведем только некоторые примеры.
Великолепный Парфенон. Древние греки оставили нам великолепные памятники архитектуры, которые доставляют современным людям такое же эстетическое наслаждение, как и их нашим далеким предкам. И среди них первое место по праву принадлежит Парфенону. Описания Парфенона всегда изобиловали только превосходными степенями. Этот храм, посвященный богине Афине Парфенос, по праву считается одним из величайших образцов античного зодчества, шедевром мирового искусства и пластики. Он построен в середине V века до н.э. скульпторами Иктином и Калликратом. Это был период высшего подъема античной культуры, и храм богини Афины на холме Акрополь по сей день гордо напоминает об этом всему миру.
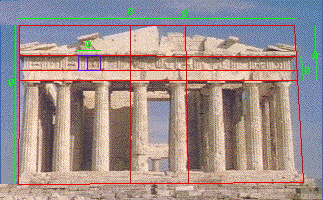
Гармонический анализ Парфенона был осуществлен многими исследователями. И хотя эти исследования несколько отличаются своими подходами, но все исследователи сходятся в главном: Парфенон отличается удивительной величественностью и глубокой человечностью архитектурных и скульптурных образов и что главной причиной красоты Парфенона является исключительная соразмерность его частей, основанная на золотом сечении (Рис.9).
Рис.9. Гармонический анализ Парфенона
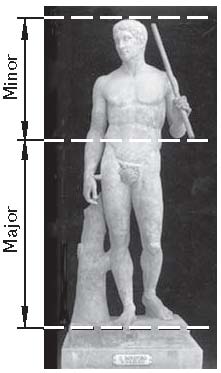
Золотое сечение в греческой скульптуре. Эталоном красоты человеческого тела, образцом гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов: Фидия, Поликлета, Мирона, Праксителя. В своих творениях греческие мастера использовали принцип золотой пропорции. Одним из высших достижений классического греческого искусства может служить статуя Дорифора, изваянная Поликлетом в 5-м веке до н.э. (Рис.10-а).
(а) (b)
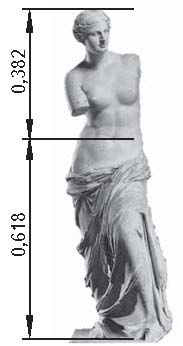
Рис.10. «Дорифор» Поликлета (а) и Венера Милосская (b)
«Дорифор» Поликлета считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами. Это тем более основательно, что именно этой скульптуре было присвоено наименование "Канон". Широкие плечи юноши почти равны высоте туловища, высота головы восемь раз укладывается в высоте тела, а золотой пропорции отвечает положение пупка на теле атлета. Отношение “major” к “minor” равно золотой пропорции.
Одним из лучших памятников греческого скульптурного искусства также является Венера Милосская - статуя богини Афродиты, найденная на острове Мелос (скульптор Агесандр из Антиохии на Медаре, ок.120 г. до н.э.). Богиня изображена скульптором полуобнаженной, так, что одеяние, закутывая ноги и низ торса, является постаментом для открытых рук, которые были показаны в движении (Рис.10-b). Венера Милосская является настоящей жемчужиной Лувра, эталоном женской красоты Древней Эллады. Гармонический анализ Венеры Милосской приводит к гармонической пропорции (0.618 : 0.382), представляющей собой «золотое сечение».
5. Золотое Сечение в искусстве Возрождения
Идея «божественной гармонии» в эпоху Возрождения
Идея гармонии оказалась в ряду тех концептуальных построений античной культуры, к которым церковь отнеслась с большой заинтересованностью. Согласно христианской доктрине Вселенная была творением Бога и беспрекословно подчинялась его воле. И христианский Бог при сотворении мира руководствовался математическими принципами. Эта католическая доктрина в науке и искусстве Возрождения приобрела форму поиска математического плана, по которому Бог создал Вселенную.
По мнению Мориса Клайна [32], именно тесное слияние религиозной доктрины о Боге как творце Вселенной и античной идеи о числовой гармонии Мироздания, стало одной из важнейших причин огромного всплеска культуры в эпоху Возрождения. Наиболее ярко главная цель науки эпохи Возрождения изложена в следующем высказывании Иоганна Кеплера:
«Главной целью всех исследований внешнего мира должно быть открытие рационального порядка и гармонии, которые Бог ниспослал миру и открыл нам на языке математики».
Искусство эпохи Возрождения (особенно живопись) в значительной степени связано с библейскими сюжетами. Ярким примером картины, написанной по библейским сюжетам, является картина «Святое семейство» Микеланджело (Рис.11). Картина справедливо признана одним из шедевров западноевропейского искусства. Это единственная работа Микеланджело, выполненная на дереве, который большую часть своего творчества посвятил скульптуре. Фигура Марии, Иосифа и младенца Христа образуют винтообразную группу, внося сильный заряд пластической энергии в композиционное целое. Картину часто называют "Тондо Дони", поскольку, во-первых, она принадлежала семейству Дони во Флоренции, а во-вторых, имеет круглую форму (по-английски "tondo"). По общепринятой гипотезе, картина была исполнена к свадьбе Аньоло Дони с Магдаленой Строцци, герб которой вырезан на раме. Произведя гармонический анализ этой картины, исследователи обнаружили, что композиционное построение картины основано на пентакле (Рис.11).

Рис.11. Картина «Святое семейство» Микеланджело
Другим примером картины, основанной на библейском сюжете, является картина «Распятие» (“Crucifixion”) еще одного знаменитого живописца эпохи Возрождения Рафаэля Санти (1483-1520). Гармонический анализ картины (Рис.12) показывает, что композиционный план этой картины основан на «золотом» равнобедренном треугольнике (Рис.12).
Рис.12. Картина Рафаэля Санти «Распятие» (“Crucifixion”)
«Давид» Микеланджело. Примером эталонной модели гармонически развитого человеческого тела является знаменитая статуя «Давида» Микеланджело (Рис.13).
Рис.13. «Давид» Микеланджело
Подобно Дорифору Поликлета, который в античную эпоху стал «Каноном» красоты мужского тела, «Давид» Микеланджело можно считать «Каноном» эпохи Возрождения. Сравнение статуи Давида (Рис.13) со статуями Дорифора и Венеры Милосской (Рис.10) не оставляет никаких сомнений в том, что все пропорции «Давида» основаны на золотом сечении!
«Мона Лиза» Леонардо да Винчи. В зале Лувра, в Париже, каждый посетитель пытается отыскать одну картину. Картина эта – знаменитая Мона Лиза или Джоконда, принадлежащая кисти Леонардо да Винчи. Создавая свой шедевр, художник использовал секрет, известный многим портретистам: вертикальная ось полотна проходит через зрачок левого глаза, то есть, в своей картине художник использовал «принцип симметрии». Но может быть причина в другом? Картина гениального художника привлекла внимание исследователей, которые обнаружили, что композиционное построение картины основано на двух золотых равнобедренных треугольниках, повернутых друг к другу своими основаниями (Рис.14). Гармонический анализ картины показывает, что зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух бисектрисс верхнего золотого треугольника, которые, с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами золотого треугольника делят их в пропорции «золотого сечения». Таким образом, Леонардо использовал в своей картине не только принцип симметрии, но и «золотое сечение»!


Рис.14. Гармонический анализ картины «Мона Лиза (Джоконда)»
В течении всей своей жизни Леонардо хранил память о своей родной матери Катерине, которая оказалась удивительно похожей на Мону Лизу, жену флорентийского купца Джокондо. И, возможно, это стало главной причиной желания Леонардо создать живописный портрет Моны Лизы. Давно не испытывал Леонардо да Винчи такого огромного прилива творческих сил. Все, что было в нем самом жизнерадостного, светлого и ясного, он вкладывал в свою работу. И всю свою сыновью любовь к своей матери Катерине, с которой он был разлучен в раннем детстве, он воплотил в своей знаменитой картине, которая определила развитие живописи на многие века вперед. И спасибо Богу за то, что он свел Мону Лизу с Леонардо да Винчи на закате жизненного пути великого художника!
«Божественная пропорция» Луки Пачоли
Культура Древней Греции и культура Рима и Византии – вот два мощных потока духовных ценностей, слияние которых дало ростки нового, титанов Ренессанса. Титан – это самое точное слово по отношению к таким людям, как Леонардо да Винчи, Микеланджело, Николай Коперник, Альберт Дюрер, Христофор Колумб, Америго Веспуччи. В эту плеяду по праву входит и математик Лука Пачоли.
Он родился в 1445 г. в провинциальном городке Борго Сан-Сеполькро, что в переводе с итальянского звучит не слишком радостно: «Город Святого Гроба».
Мы не знаем, сколько лет было будущему математику, когда его отдали учиться в мастерскую художника Пьеро делла Франческо, слава которого гремела по всей Италии. Это была первая встреча юного дарования с великим человеком. Пьеро делла Франческо был художником и математиком, но только вторая ипостась учителя нашла отзвук в сердце ученика. Юный Лука, математик от Бога, был влюблен в мир чисел, число представлялось ему некоторым универсальным ключом, одновременно открывающим доступ к истине и красоте.
Второй великий человек, встретившийся на жизненном пути Луки Пачоли, был Леон Баттиста Альберти – архитектор, ученый, писатель, музыкант. Глубоко западут в сознание Л.Пачиоли слова Альберта:
«Красота есть некое согласие и созвучие частей в том, частями чего они являются, - отвечающие строгому числу, ограничению и размещению, которых требует гармония, то есть абсолютное и первичное начало природы».
Влюбленный в мир чисел, Л. Пачоли повторит за Пифагором мысль о том, что число лежит в основе Вселенной.
В 1472 г. Лука Пачоли осуществляет пострижение в монахи францисканского ордена, что дало ему возможность заниматься наукой. События показали, что он сделал правильный выбор. В 1477 г. он получает профессорское кресло в университете Перуджи.
Педагогический труд Пачоли сочетает с научной работой: он начинает писать энциклопедический труд по математике. В 1494 г. этот труд выходит в свет под названием «Сумма арифметики, геометрии, учения о пропорциях и отношениях». Монументальная печатная работа Л. Пачоли, несомненно, способствовала его славе. Когда в 1496 году в Милане – крупнейшем городе и государстве Италии - в университете открыли кафедру математики, занять ее был приглашен Лука Пачоли.
В это время Милан был центром науки и искусства, в нем жили и творили выдающиеся ученые и художники – и одним из них был Леонардо да Винчи, который стал третьим великим человеком, встретившимся на жизненном пути Луки Пачоли. Под непосредственным влиянием Леонардо да Винчи он начинает писать свою вторую великую книгу ” Divine Proportione” («Божественная пропорция»).
Рис.15. Титульные страницы книги Луки Пачиоли «Divina Proportione» (1509) и книги Алексея Стахова «The Mathematics of Harmony» (2009)
Книга Л. Пачоли, изданная в 1509 г., оказала заметное влияние на современников. Изданный ин-кварто фолиант Пачоли был одним из первых прекрасных образцов книгопечатного искусства Италии. Историческое значение книги состояло в том, что это было первое математическое сочинение, целиком посвященное «золотому сечению». Книга проиллюстрирована 60 (!) великолепными рисунками, выполненными самим Леонардо да Винчи. Это означает, что книга Пачоли имеет не только научную, но и художественную ценность.
Эта книга является одним из первых математических сочинений, в котором христианская доктрина о Боге как творце Вселенной получает научное обоснование.
В 1510 г. Луке Пачоли исполнилось 65 лет. Он устал, постарел. В библиотеке Болонского университета хранится рукопись неизданной работы Л. Пачоли «О силах и количествах». В предисловии мы находим печальную фразу: «приближаются последние дни моей жизни». Он умер в 1515 г. и похоронен на кладбище своего родного города Сан-Сеполькоро.
После смерти труды великого математика оказываются преданными забвению почти на четыре столетия. И когда в конце 19-го века его труды стают всемирно известными, благодарные потомки после 370-летнего забвения на его могиле поставили памятник, на котором написали:.
«Луке Пачоли, который был другом и советником Леонардо да Винчи и Леона Баттиста Альберти, который первый дал алгебре язык и структуру науки, который применил свое великое открытие к геометрии, изобрел двойную бухгалтерию и дал в математических трудах основы и неизменные нормы для последующих поколений».
Любопытно сравнить книгу Луки Пачоли и книгу Алексея Стахова (Рис.15). Между ними есть много общего. Книга Луки Пачоли является первой в истории науки книгой, посвященной «золотому сечению» («божественной пропорции»). Книга Алексея Стахова является первой в истории науки книгой, посвященной «Математике Гармонии», в основе которой лежит «золотое сечение». Связь между этими книгами подчеркивается изображением картины «Лука Пачоли» (художник Якопо де Барбари) на титульной странице книги Стахова. Но прямо-таки мистическое впечатление производит еще один факт, связывающий эти книги: временное расстояние между ними составляет ровно 500 лет (2009 - 1509 = 500)!
Литература
-
Coxeter, H. S. M. Introduction to Geometry. New York: John Wiley and Sons, 1961.
-
Воробьев Н.Н. Числа Фибоначчи. М.: Наука, 1984. (первое издание - 1961).
-
Hoggat V. E. Jr. Fibonacci and Lucas Numbers. - Boston, MA: Houghton Mifflin, 1969.
-
Vajda S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. - Ellis Harwood Limited, 1989.
-
-
Стахов А.П. Введение в алогоритмическую теорию измерения. М.: Советское радио, 1977.
-
Стахов А.П. Коды золотой пропорции. М.: Радио и связь, 1984.
-
Сороко Э.М. Структурная гармония систем. Минск: Наука и техника, 1984.
-
Grzedzielski Jan. Energetycno-geometryczny kod Przyrody. Warszawa: Warszwskie centrum studenckiego ruchu naukowego, 1986 (in Polen).
-
Васютинский Н.А. Золотая пропорция. М.: Молодая Гвардия», 1990.
-
Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. Три взгляда на гармонию природы. М.: Стройиздат, 1990.
-
Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов: Свит, 1994.
-
Dunlap R.A. The Golden Ratio and Fibonacci Numbers. World Scientific, 1997.
-
Коробко В.И. Золотая пропорция и проблемы гармонии систем. М.: Изд-во Ассоциации строительных вузов стран СНГ, 1998.
-
Шевелев И.Ш. Метаязык живой природы. М.: Воскресенье, 2000.
-
Kappraff Jay. Connections. The geometric bridge between Art and Science. Second Edition. Singapore, New Jersey, London, Hong Kong: World Scientific, 2001.
-
Kappraff Jay. “Beyond Measure. A Guided Tour Through Nature, Myth and Number”. Singapore, New Jersey, London, Hong Kong: World Scientific, 2002.
-
Olsen Scott. The Golden Section: Nature’s Greatest Secret. New York: Walker Publishing Company, 2006.
-
Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. Санкт-Петербург: Питер, 2006.
-
Шевелев И.Ш. Основы гармонии. Визуальные и числовые образы реального мира. М.: Луч, 2009.
-
-
Аракелян Грант. Теория ЛМФ и принцип золотого сечения. В 4 частях. Академия Тринитаризма, 2011 (электронная публикация).
-
Григорьев Ю., Мартыненко Г. Типология последовательностей Фибоначчи: Теория и приложения. Введение в математику гармонии. LAMBERT Academic Pudlishing Gmbh & Co.KG. Saarbruecken, Germany, 2012.
-
Волошинов А. В. Математика и искусство. М., Просвещение, 2000.
-
Stakhov A.P. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science. New Jersey, London, Singapore, Hong Kong: World Scientific, 2009.
-
Шестаков В.П. Гармония как эстетическая категория. М.: Наука, 1973.
-
Пьер Тейяр де Шарден. Феномен человека. Перевод и примечания Н.А.Садовского - М.: "Прогресс", 1965.
-
Дарио Салас Соммэр. Мораль XXI века. М.: Издательский дом «София», 2004.
-
Дарио Салас Соммэр. Развитие внутреннего мира. Москва: Научная книга, 2008.
-
Дарио Салас Соммэр, От Золотой Математики к Золотому Поведению //«Академия Тринитаризма», М., Эл № 77-6567, публ.15105, 20.02.2009
-
Дарио Салас Соммэр, А.П. Стахов, «Золотая» Герметическая Философия //«Академия Тринитаризма», М., Эл № 77-6567, публ.15144, 09.03.2009
-
Клайн М. Математика. Утрата определенности (пер. с англ.). Москва: Мир, 1984.
-
Колмогоров А.Н. Математика в ее историческом развитии. М.: Наука, 1991.
-
-
Dimitrov Vladimir. A new kind of social science. Study of self-organization of human dynamics. Morrisville Lulu Press, 2005.
-
Herz-Fischler, Roger. A Mathematical History of the Golden Number. New York: Dover Publications, Inc., 1998.
-
Петухов С.В. Матричная генетика, алгебры генетического кода, помехоустойчивость. Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008.
-
Лосев А. История философии как школа мысли. Коммунист, 1981, №1.
-
Веннинджер М. Модели многогранников. Пер. с англ. М.: Мир, 1974.
-
Stakhov A.P. The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М.: Наука, 1989.
-
Гика Матила. Эстетика пропорций в природе и искусстве (пер. с фр.). Москва: Издательство Академии Архитектуры , 1936.
-
Гримм Г.Д. Пропорциональность в архитектуре. Ленинград-Москва: ОНТИ, 1935.
-
Gardner Martin. Mathematics, Magic and Mystery. New York: Publishing House “Dover”, 1952.
-
Пойа Д. Математическое открытие (перевод с англ.). М.: Наука, 1970. (английское издание, том 1, 1962, том 2, 1965)
-
-
Vera W. de Spinadel. From the Golden Mean to Chaos. Nueva Libreria, 1998 (second edition, Nobuko, 2004).
-
Gazale Midhat J. Gnomon. From Pharaohs to Fractals. Princeton, New Jersey: Princeton University Press, 1999 (Русский перевод: Мидхат Газале. Гномон. От фараонов до фракталов. Москва-Ижевск: Институт компьютерных исследований, 2002.)
-
Татаренко А.А. Золотые Tm – гармонии и Dm – фракталы — суть солитоно-подобного Тm – cтруктурогенеза мира // «Академия Тринитаризма», М., Эл № 77-6567, публ.12691, 09.12.2005
-
Аракелян Грант. Числа и величины в современной физике. Ереван: Изд. АН, 1989.
-
Шенягин В.П. «Пифагор, или Каждый создает свой миф» - четырнадцать лет с момента первой публикации о квадратичных мантиссовых s-пропорциях // «Академия Тринитаризма», М., Эл № 77-6567, публ.17031, 27.11.2011
-
Falcon Sergio, Plaza Angel. On the Fibonacci k-numbers Chaos, Solitons & Fractals, Volume 32, Issue 5, June 2007 : 1615-1624.
-
-
A. Stakhov, S. Aranson, “Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem.” Applied Mathematics, 2011, No.1 (January), No.2 (February), No.3 (March).
-
Стахов, А.П. Формулы Газале, новый класс гиперболических функций Фибоначчи и Люка и усовершенствованный метод «золотой» криптографии // «Академия Тринитаризма», М.,Эл № 77-6567, публ.14098, 21.12.2006
-
-
-
-
-
G. Bergman, A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98-119.
-
A.P. Stakhov, “The Golden Section in the Measurement Theory,” Computers & Mathematics with Applications, 1989, Vol. 17, No 4-6, 613-638.
-
A.P. Stakhov, “Generalized golden sections and a new approach to geometric definition of a number. Ukrainian Mathematical Journal, vol. 56, 2004:-1143 – 1150 (Russian).
-
A.P. Stakhov, “Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic” // The Computer Journal, 2002, Vol. 45, No. 2, 221-236.
-
A.P. Stakhov, “A generalization of the Fibonacci Q-matrix” // Reports of the National Academy of Sciences of Ukraine, 1999, No 9, 46-49.
-
-
A.P. Stakhov, The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
. Stakhov, “The “golden” matrices and a new kind of cryptography.” Chaos, Solitons & Fractals 2007, Volume 32, Issue 3, 1138-1146.
-
A. Stakhov, S. Aranson. “Golden” Fibonacci Goniometry. Fibonacci-Lorentz Transformations, and Hilbert’s Fourth Problem. Congressus Numerantium, 193 (2008), 119-156.
-
A.P. Stakhov, “The Golden Section and Modern Harmony Mathematics.” Applications of Fibonacci Numbers, Kluwer Academic Publishing, Volume 7, 1998: 393-399.
-
Стахов А. П., Ткаченко И. С. Гиперболическая тригонометрия Фибоначчи // Доклады Академии наук УССР, том 208, № 7, 1993.
-
Stakhov A., Rozin B. On a new class of hyperbolic function // Chaos, Solitons & Fractals, 2005, Vol. 23, Issue 2, 379-389.
-
Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. // Украинский математический журнал, 2004, Vol. 56, No. 8, 1143-1150.
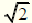 , равное отношению диагонали к стороне квадрата. С этим числом связано открытие несоизмеримых отрезков и история наиболее драматичного периода в античной математике, который привел к разработке теории иррациональностей и иррациональных чисел и в конечном итоге – к созданию современной «непрерывной» математики.
, равное отношению диагонали к стороне квадрата. С этим числом связано открытие несоизмеримых отрезков и история наиболее драматичного периода в античной математике, который привел к разработке теории иррациональностей и иррациональных чисел и в конечном итоге – к созданию современной «непрерывной» математики.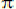 лежит в основе тригонометрических функций и тригонометрии, а число е лежит в основе так называемых гиперболических функций, которые были использованы Николаем Лобачевским при описании математических соотношений созданной им «гиперболической геометрии», которая считается наиболее крупным математическим открытием 19 в.
лежит в основе тригонометрических функций и тригонометрии, а число е лежит в основе так называемых гиперболических функций, которые были использованы Николаем Лобачевским при описании математических соотношений созданной им «гиперболической геометрии», которая считается наиболее крупным математическим открытием 19 в. (1)
(1)
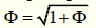 (9)
(9)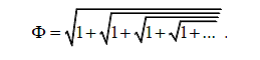 . (10)
. (10)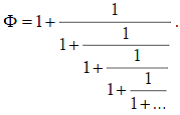 . (11)
. (11)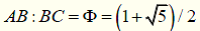
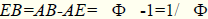 .
.