Онтологические прогулки

1. Введение

Так случилось в моей жизни, что я избрал нелегкий путь ученого. Жалею ли я, что я избрал этот сложный и тернистый путь? Нет, не жалею. И если бы мне пришлось выбирать свой жизненный путь снова, я повторил бы его опять.

Мне было очень трудно, особенно на начальном этапе своего пути. Я пробивался в своей жизни, как говорится, «от сохи». Я испытал в своей жизни холод и голод и достиг научных вершин только благодаря своему таланту и трудолюбию. Но я не мог бы сделать это без тех людей, которые шли со мной рядом и в любой момент готовы были подставить мне плечо в трудные минуты. Многих из них уже нет в живых. И грузят безвозвратные утраты мое сердце. Я хотел бы сказать людям, ставшим для меня примерами Доброты, Нравственности и Человеколюбия, большое человеческое спасибо.

Преклоняю голову перед памятью своего деда, бедного черниговского крестьянина Стаха Харитона Ивановича, которого в поисках лучшей доли еще в 20-годы прошлого столетия судьба забросила на Херсонщину. Только благодаря этому событию я и появился на белый свет, потому что мой отец Петр полюбил скромную девушку Дарью из рода Щербаковых на Херсонщине. Дед научил меня добру и нравственному отношению к людям.

Низкий поклон моему отцу, бойцу Харьковского студбата Стахову Петру Харитоновичу. Он погиб в октябре 1941 г. на подступах  к Москве, защищая Родину от фашистских захватчиков. Рассказы о нем моего деда и моей мамы с детства запали в душу, и отец навсегда остался в моей душе высшим нравственным критерием.

Моей маме, сельской учительнице Стах Дарье Харитоновне, научившей меня читать и писать в 5-летнем возрасте, я обязан ранним приобщением к письменности, образованию и науке. И я рад, что своими научными успехами оправдал ее надежды.

 Мое взросление и духовное воспитание происходило под влиянием моего брата Георгия Щербакова. Я всегда стремился быть таким, как мой брат, и поступать всегда так, как поступил бы мой брат.

Я склоняю свою голову перед своей женой Антониной Стаховой (Севериловой), любящей и бесконечно преданной. Она родила мне двух замечательных детей, Дмитрия и Анну, взяла на свои хрупкие плечи все семейные тяготы и дала мне возможность безраздельно отдаться научному творчеству. И все величие своей души она проявила в самые сложные периоды нашей жизни, особенно в периоды наших многолетних «африканских путешествий» - и я благодарен ей за все это.

После переезда в Канаду неоценимую помощь в моей научной деятельности оказала дочь Анна Слученкова (Стахова), вместе с которой мы еще в 2001 г. выставили на Интернете Музей Гармонии и Золотого Сечения . Но особенно большую помощь она оказала мне при написании книги Alexey Stakhov. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science (World Scientific, 2009).  Эта книга является первой в истории науки книги по “математике гармонии». И эта книга принесла мне мировую известность.

***

Мне очень повезло в тот момент, когда я принял решение вступить на стезю науки. На моем пути появился «Учитель». Им стал выдающийся ученый и человек большой души Александр Андреевич Волков. Я поступил в аспирантуру кафедры технической кибернетики Харьковского института радиоэлектроники в 1963 г. Моим научным руководителеп стал А.А. Волков, который в тот момент возглавлял кафедру технической кибернетики. В 1966 г. под научным руководством А.А. Волкова я защитил кандидатскую диссертацию, а в 1972 г. – докторскую диссертацию. И в этом – огромная заслуга Александра Андреевича. И я пронес сквозь всю свою жизнь чувство глубокой признательности и благодарности своему Учителю.

Я всю жизнь учился. И на моем пути встречались замечательные люди, которые способствовали моему научному и профессиональному росту. Я по настоящему оценил математику как «Метод Мышления» после встречи с выпускником механико-математического факультета Львовского университета Игорем Витенько, который без всякого преувеличения мог бы стать выдающимся математиком и славой Украины, если бы не ушел из жизни так рано. Его трагическая смерть в октябре 1974 г. (он покончил с собой, выразив тем самым протест против бездушной партийной верхушки Ужгородской области и Ужгородского университета, которая травила его в течение многих лет за то, что его отец был «бандеровцем») стала для меня личной трагедией и тяжелейшей утратой. Своим учителем философии я считаю выдающегося русского философа и ученого энциклопедических знаний Георгия Васильевича Чефранова.

Таким образом, моими научными достижениями я обязан, прежде всего,  трем выдающимся личностям, встретившимся на моем жизненном пути:

1. Доктору технических наук, профессору Волкову Александру Андреевичу. Проф. Волков подготовил около 100 кандидатов наук и 20 докторов наук, и я стал одним из первых докторов наук, подготовленных им.

2. Кандидату физико-математических наук доценту Игорю Владимировичу Витенько, от которого я получил большой багаж знаний в области математики и благодаря которому я по существу стал математиком.

3. Доктору философских наук профессору Георгию Васильевичу Чефранову (математику по образованию), который привил мне любовь к философии и философским основам математики. Память об этом замечательном человеке навсегда останется в моей душе. И именно ему посвящена эта моя статья.

2. Таганрогский радиотехнический институт

Партийное взыскание

В конце 1970 года я написал письмо ректору Таганрогского радиотехнического института профессору Каляеву Анатолию Васильевичу с просьбой предоставить мне работу в институте. По его просьбе я приехал в Таганрог и продемонстрировал экземпляр своей докторской диссертации. Я думаю, что знакомство со мной и моей диссертацией его удовлетворило, потому что совершенно неожиданно для меня я получил от него весьма лестное предложение возглавить кафедру информационно-измерительной техники. Для этого он попросил меня подготовить все необходимые документы для избрания меня по конкурсу. Одним из этих документов была так называемая "производственная характеристика" о моей научной и педагогической деятельности в Харьковском институте радиоэлектроники, где я работал в тот период в качестве доцента. Согласно закону о трудовом законодательстве институт должен был выдать мне объективную характеристику по первому моему требованию. Однако КПСС жила по своим законам, которые не всегда согласовывались с трудовым законодательством.

В начале 1971 года я обратился в ректорат и партком ХИРЭ с просьбой выдать мне производственную характеристику для избрания на должность зав. кафедрой информационно-измерительной техники Таганрогского радиотехнического института. В выдаче характеристики мне было отказано. Мои многократные обращения в ректорат, партком, Минвуз Украины, райком и даже обком партии ни к чему не привели. И тогда я принял решение предоставить в Таганрогский радиотехнический институт свою производственную характеристику, подписанную ректором и секретарем парткома, но выданную мне для других целей. Я рассуждал следующим образом. Таганрогскому радиотехническому институту требовалась объективная характеристика о моей работе в Харьковском институте радиоэлектронике – и такая характеристика у меня была. Отказывая в выдаче производственной характеристики, ректорат и партком ХИРЭ нарушали трудовое законодательство. Поэтому я не видел в своих действиях никакого «криминала». О своем решении я проинформировал ректора и секретаря парткома ХИРЭ. Секретарь парткома пригрозил мне, что за этот поступок я буду исключен из рядов КПСС. В этой ситуации я начал действовать как истинный телец. Я принял "решение" - и никакие угрозы секретарей парткомов уже не могли его изменить.  

В начале февраля 1971 года я получил информацию из Таганрога о том, что я единогласно избран на должность зав. кафедрой информационно-измерительной техники. После этого началась заключительная стадия моей "харьковской драмы". Партком ХИРЭ начал "раскручивать" мое партийное дело с целью исключения меня из рядов КПСС. Меня обвинили в том, что я обманул партийную организацию (хотя я всех честно проинформировал о своих действиях). Поскольку на исключение из партии мое дело явно “не дотягивало", то решением парткома мне был объявлен строгий партийный выговор с занесением в учетную карточку с формулировкой "за обман партийной организации" (хотя я никого не обманывал – и все это прекрасно понимали). Но на моем примере надо было «настращать» других – и эту задачу партком института успешно выполнил. В результате я получил одно из самых строгих партийных взысканий, следующим за ним было уже исключение из партии. Эта история с партийным выговором стала для меня хорошим жизненным уроком. Я понял, что партия может расправиться с любым ее членом, независимо от его званий и заслуг, и в дальнейшем я вел себя достаточно осторожно и взвешенно в подобных острых ситуациях.

Кафедра информационно-измерительной техники Таганрогского радиотехнического института

Я проработал в Таганрогском радиотехническом институте сравнительно небольшой период – с 1971 по 1977 годы. Но этот период для меня был насыщен огромным количеством событий, которые определили всю мою дальнейшую научную судьбу. Достаточно назвать такие из них, как защита докторской диссертации (1972 г.), присвоение ученого звания профессора (1974 г.), научная стажировка в Австрии (Венский технический университет, 1976 г.), начало уникального по своим масштабам зарубежного патентования моих изобретений по «компьютерам Фибоначчи», публикация моей первой книги «Введение в алгоритмическую теорию измерения» (Советское радио, 1977 г.) и др.

Таганрогский радиотехнический институт в тот период считался одним из ведущих научно-учебных центров страны в области радиоэлектроники. В 1977 г. ТРТИ праздновал свое 25-летие, и я назвал бы тот славный период в работе ТРТИ, который предшествовал его 25-летию, «научно-романтическим» периодом. Ректором института был Анатолий Васильевич Каляев, крупнейший ученый, создатель одного из перспективных направлений в области компьютерной техники. В этот период научная жизнь в ТРТИ бурлила, защищались многочисленные кандидатские, а затем и докторские диссертации, а ежегодно в Таганроге проводилась масса научных семинаров, симпозиумов, Всесоюзных и международных конференций в области радиоэлектроники и компьютерной техники, куда приезжали поплескаться в Азовском море и погреться в лучах южного солнца, а заодно и поделиться новыми научными идеями многие знаменитые ученые.

На кафедре мне работалось очень легко. В ее состав входили преподаватели, многие из которых были значительно старше меня по возрасту. Одной из самых светлых личностей был Виктор Ильич Богданов, который в свое время был ректором института и который пользовался огромным уважением в институте. Все преподаватели кафедры были хорошими методистами, лекторами, фанатиками учебного процесса, прекрасными воспитателями студенческой молодежи.

Главной моей задачей стало развитие научного направления и подготовка научных кадров. В то время в институте решением Ученого Совета были введена так называемая ПНИРС (плановая научно-исследовательская работа студентов). Я активно включился в эту деятельность и организовал студенческий научный кружок, который с огромным энтузиазмом посещали лучшие студенты нашей кафедры. Назову только некоторых из них: Юрий Вишняков, Алексей Азаров, Владимир Лужецкий, Владимир Онопко, Николай Соляниченко, Александр Фомичев и многие другие. Именно они стали моими первыми аспирантами в ТРТИ. Начались защиты кандидатских диссертаций. За неполные 7 лет под моим научным руководством защитили кандидатские диссертации 7 аспирантов; трое из них проф. Ю.М. Вишняков, декан факультета автоматики и вычислительной техники, и доценты В.Г. Косторниченко, В.Г. Галалу продолжают успешно работать в университете.

2. Мое знакомство с Георгием Васильевичем Чефрановым

Профессура Таганрогского радиотехнического института

В Таганроге в тот период работало много замечательных докторов наук, профессоров очень высокого научного уровня. Всех нас объединял специальный "профессорский" философский семинар, который возглавлял Виктор Ильич Богданов и который проводился регулярно (один раз в месяц). К семинару все мы относились очень ответственно, и после нескольких выступлений на этом семинаре по философским проблемам науки (в частности, по философским проблемам математики и теории информации) все таганрогские профессора меня глубоко "зауважали".

Профессорская среда ТРТИ отличалась высокой интеллигентностью. Например, кафедру химии возглавлял профессор Алексей Николаевич Харин, автор вузовского учебника по химии. Но он одновременно был прекрасным музыкантом и музыковедом. На фортепианные концерты профессора Харина, которые он давал раз, а то и два раза в год, собирались все студенты и сотрудники. Можно себе представить, каким огромным уважением пользовался профессор Харин среди студентов и сотрудников. В институте в тот период работал Аскольд Николаевич Мелихов, который был одной из самых ярких звезд советской компьютерной науки и самым молодым советским доктором наук в этой области. Всегда с огромным уважением вспоминаю проф. Соловьева Александра  Ивановича, автора многочисленных книг по механике; он возглавлял в тот период кафедру механики, а также проф. Владимира Александровича Малышева, с которым нас связывали чувства искренней дружбы и уважения.

Именно на этом «профессорском» семинаре я и познакомился с Георгием Васильевичем Чефрановым.  

Георгий Васильевич Чефранов

Доктор философских наук профессор Георгий Васильевич Чефранов был одним из самобытных таганрогских ученых, автором интересных философских идей и многих философских книг с необычными названиями, например, «Бесконечность и интеллект».

Небольшая биографическая справка о Г.В. Чефранове, взятая из сайта кафедры философии Таганрогского радиотехнического университета (ныне Таганрогский кампус ЮФУ) http://sfedu.ru/www/rsu$elements$.info?p_es_id=-3000000001958, гласит следующее:

«Несколько подробнее следует сказать о жизни и деятельности Чефранова Георгия Васильевича (27.02.1922 г., г. Ахтырка Сумской обл. — 01.04.1991, г. Таганрог). В 1948 г. он окончил физико-математический факультет Казанского государственного университета по специальности астрономия. Работал в г. Ленинграде, одновременно экстерном сдал курс философского факультета и был приглашен в аспирантуру, которую окончил в 1952 г. По путевке МВО был направлен в ТРТИ, где начал работать с1953г. в должности ассистента кафедры высшей математики. С 1956 г. перешел работать на кафедру марксизма-ленинизма, где преподавал философию. С созданием кафедры философии и научного коммунизма Георгий Васильевич сочетает выполнение обязанностей заведующего кафедрой и преподавательскую деятельность. Чефранов В.Г. на лекциях и семинарских занятиях стремился развивать у студентов творческий подход в усвоении сложных теоретических проблем естествознания и обществоведения. Много внимания уделял самостоятельной и научной работе студентов. Для аспирантов был разработал спецкурс по философским проблемам естествознания. В научных исследованиях Чефранов Г.В. проявил большую работоспособность. Основным содержанием его научных работ являлась проблема бесконечного. Этой проблеме была посвящена кандидатская диссертация: "Некоторые вопросы бесконечности пространства - времени", успешно защищенной в 1961 г. в МГУ. Этой же теме посвящены его публикации 60-х, начала 70-х годов, в том числе монография "Бесконечность и интеллект" (изд-во Ростовского госуд. ун-та, 1971 г., 11 п.л.). В ноябре 1972 г. Чефранов Г. В. успешно защитил докторскую диссертацию по теме "Проблемы моделирования бесконечности".

Из этой справки мы узнаем много интересного о Чефранове. Прежде всего, мы узнаем, что Георгий Чефранов окончил физико-математический факультет Казанского государственного университета по специальности астрономия, но затем, работая в Ленинграде, экстерном сдал курс философского факультета и был приглашен в аспирантуру, которую окончил в 1952 г. По путевке МВО был направлен в ТРТИ, где начал работать с 1953 г. в должности ассистента кафедры высшей математики. Но затем он перешел на кафедру марксизма-ленинизма, где преподавал философию. С созданием кафедры философии и научного коммунизма Георгий Васильевич сочетает выполнение обязанностей заведующего кафедрой и преподавательскую деятельность.

И еще одна важная деталь. Основным направлеием его научных исследований являлась проблема бесконечного. Этой проблеме была посвящена его кандидатская диссертация: "Некоторые вопросы бесконечности пространства - времени", успешно защищенная в 1961 г. в МГУ, и его докторская диссертация, защищенная в 1972 г. по теме "Проблемы моделирования бесконечности".

Поскольку «проблема бесконечности» является весьма трудной философской проблемой и не часто выбирается философами в качестве темы научных исследований, то есть все основания предположить, что доктор философских наук Г.В. Чефранов, повидимому, был ведущим советским специалистом в этой области философии.

3. Проблема бесконечного в математике

Что такое «математическая бесконечность»?

Прежде всего, следует отметить, что в математике нет единого определения понятия «бесконечность», хотя, как утверждает знаменитый немецкий математик Герман Вейль, «математика – это наука о бесконечном».

Чтобы понять хотя бы в общих чертах суть научной проблемы, изучению которой Георгий Чефранов посвятил свою жизнь, разберем это понятие более детально. В процессе развития математики сформировались следующие подходы к этому понятию: арифметическая и геометрическая, потенциальная и актуальная бесконечности. Что это такое?

Последовательность  натурального ряда чисел

1, 2, 3, …,                                                                   (1)

представляет собой первый и самый известный пример бесконечного множества. Каждое натуральное число может быть представлено в виде n=1+1+1+...+1. Уже со времен Гегеля арифметическую бесконечность натурального ряда 1+1+1+ … в силу ее бесперспективности именуют «плохой» или «дурной» бесконечностью.

            Геометрическая бесконечность состоит в неограниченном делении отрезка пополам. Паскаль писал по поводу геометрической бесконечности следующее: «Нет геометра, который бы не полагал, что пространство делимо до бесконечности. Без этого нельзя ему обойтись, как человеку нельзя быть без души. И тем не менее нет человека, который понимал бы бесконечную делимость …».

            Кроме различия ариметической и геометрической бесконечности, существует различие актуальной и потенциальной бесконечности. Для рассмотрения различий между этими понятиями вновь обратимся к натуральному ряду (1). Этот ряд можно рассматривать по-разному. Во-первых, мы можем представить натуральный ряд как «завершенный» ряд, заданный всеми своими членами одновременно. Такое представление о бесконечном называется актуальной бесконечностью.

Но натуральный ряд можно представить как ряд «развивающийся», «строящийся» по принципу n+1. Это означает, что каждое натуральное число может быть получено из предыдущего путем добавления к нему единицы. Такое представление о бесконечном называется потенциальной бесконечностью.

"Infinitum Actu Non Datur"

Как известно, математика превратилась в дедуктивную науку в Древней Греции. Уже в 6 в. до н.э. греческие философы разрабатывали проблему бесконечного и связанную с ней проблему непрерывного и дискретного. Большое внимание развитию этого понятия уделял Аристотель. Он был первым, кто категорически начал возражать  против использования актуальной бесконечности в науке, ссылаясь на то, что, зная способы счета конечного числа объектов, нельзя эти способы распространять на бесконечные множества. Аристотелю принадлежит знаменитый тезис "Infinitum Actu Non Datur", что в переводе с латинского означает утверждение о невозможности существования логических или математических (т.е. всего лишь мыслимых, а не существующих в природе) актуально-бесконечных множеств.

 Большое влияние на развитие понятия бесконечности сыграли знаменитые «Апории Зенона», указывающие на логические трудности, связанные с гипотезой о бесконечной делимости отрезков пути и времени. Рассмотрим только одну из них, называемую «Дихотомией». В этой апории Зенон утверждает, что движение невозможно, ибо до того, как движущееся тело пройдет расстояние от точки А до точки В, оно должно пройти половину этого расстояния, а перед этим четверть, одну восьмую и т.д.. Но поскольку последовательность таких отрезков бесконечна, то это значит, что точка В никогда не будет достигнута. Парадокс (апория), выдвигаемый как непреодолимый логический тупик, состоит в том, что сумма бесконечного множества слагаемых конечна.

4. Теория бесконечных множеств Кантора

            Немецкому математику Георгу Кантору (1845-1918) суждено было стать «возмутителем спокойствия» в математике 19-го века. Главным достижением Кантора стало создание теории бесконечных множеств. И главная его идея состояла в решительном отказе от тезиса Аристотеля "Infinitum Actu Non Datur" и рассмотрении бесконечных множеств, как актуально бесконечных множеств. В основу исследования бесконечных множеств Кантор положил идею взаимно однозначного соответствия элементов сравниваемых множеств. Если между элементами двух множеств можно установить такое соответствие, то говорят, что множества имеют одну и ту же мощность, то есть, они являются равномощными или эквивалентными. «В случае конечных множеств, - писал Кантор, -  мощность совпадает с количеством элементов». Вот почему мощность называют также кардинальным (количественным) числом данного множества. Указанный подход привел Кантора ко многим парадоксальным выводам, резко противоречащим нашей интуиции и здравому смыслу. Так, в отличие от конечных множеств, на которые распространяется евклидова аксиома «Целое больше части», бесконечные множества этой аксиоме не подчиняются. Легко, например, установить равномощность множества натуральных чисел и его части – множества четных чисел путем установления следующего взаимно однозначного соответствия:

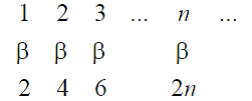
            Эта характерная черта любого бесконечного множества может быть положена в основу его определения: множество называется бесконечным, если оно равномощно с одним из своих подмножеств. Конечным же называется множество, не эквивалентное ни одному из своих подмножеств. Любое множество, эквивалентное множеству натуральных чисел, называется счетным, так  как его элементы можно занумеровать.

            Еще более поразительным оказалось другое открытие, сделанное Кантором в 1873 г. Все три множества – натуральных чисел, рациональных чисел, алгебраических чисел – имеют одну и ту же мощность, иначе говоря, множество рациональных чисел и множество алгебраических чисел являются счетными множествами.

            До Кантора считалось, что прямая содержит меньше точек, чем плоскость. Однако в 1886 г. он доказал, что в единичном квадрате не больше точек, чем в единичном отрезке. Таким образом, мощность двумерного континуума оказалась равной мощности континуума одного измерения.

            Уже из изложенного можно сделать вывод, что в отличие от большинства своих предшественников Кантор первый предпринял прямое и широкое исследование самой математической бесконечности, получив совершенно новые, неожиданные результаты.

            Канторовская теория бесконечных множеств  вызвала бурю протестов уже в 19 в. Детальный анализ критики этой теории проведен в главе «Изгнание из рая: новый кризис в основаниях математики» книги Мориса Клайна [1]. Многие известные математики 19 в. высказались резко отрицательно по поводу этой теории. Леонид Кронекер (1823-1891), испытывавшей личную неприязнь к Кантору, назвал его шарлатаном. Анри Пуанкаре (1854-1912) называл теорию множеств «тяжелой болезнью» и считал ее своего рода «математической патологией». В 1908 г. он заявил:

            «Грядущие поколения будут рассматривать теорию множеств как болезнь, от которой они излечились».

            К сожалению, у теории Кантора были не только противники, но и сторонники. Рассел назвал Кантора одним из великих мыслителей 19 в. В 1910 г. Рассел написал: «Решение проблем, издавна окутывавших тайной математическую бесконечность, является, вероятно, величайшим достижением, которым должен гордиться наш век». Рассела поддержал Гильберт, заявив, что  «никто не изгонит нас из рая, созданного Кантором».

То, что Кантор своей теорией множеств произвел революцию в математике, общеизвестно. Кульминационным пунктом в признании канторовской теории множеств можно считать конец 19-го века, когда математика приняла теорию множеств в качестве своей логической базы. Официальное провозглашение теоретико-множественных представлений фундаментом математики состоялось в 1897 г.: оно содержалось в речи Ж. Адамара на 1-м Международном конгрессе математиков в Цюрихе. В лекции Адамара подчеркивалось, что основная привлекательная причина теории множеств состоит в том, что впервые в истории математики была проведена классификация множеств на основе новоизобретенного понятия «мощности» и получены поразительные математические результаты, которые воодушевляли математиков на новые и удивительные открытия.

Обнаружение парадоксов в Канторовской теории множеств

            Но не успели математики насладиться «математическим раем», предоставленным им Кантором своей теорией бесконечных множеств, как спустя уже несколько лет после 1-го Международного конгресса математиков в теории множеств были обнаружены парадоксы или антиномии (от греческих слов «анти» - против и «номос» - закон), которые стали основой очередного, третьего по счету (после открытия несоизмеримых отрезков и обоснования теории пределов) кризиса в основаниях математики, который не преодолен и до настоящего времени.

            Один из этих парадоксов был обнаружен знаменитым английским философом Бертраном Расселом (1872-1970). Сам Рассел демонстрирует обнаруженный им парадокс на примере «деревенского парикмахера», который дал обещание брить всех тех и только тех жителей своей деревни, которые не бреются сами. Таким путем парикмахер разбивал множество жителей деревни на два подмножества. Спрашивается: должен ли он брить самого себя? То есть, к какому из двух подмножеств парикмахер должен отнести себя? Если он будет брить себя, значит, он тем самым включает себя в число тех, которые бреются сами, и тогда он не должен брить себя; если же он не будет брить себя, то он уже будет принадлежать к тем, которые сами себя не бреют, и значит, он должен брить себя. Получается логическое противоречие, недопустимое в математике!

Как упоминалось, возникновение антиномий в теории множеств породило новый, третий по счету глубокий кризис основ математики [1]. Были предприняты различные попытки преодоления этого кризиса. Наиболее радикальным из них является конструктивное направление в математике [2]. Представители конструктивного анализа увидели основную причину парадоксов канторовской теории множеств в использовании понятия «актуальная бесконечность». Наиболее убедительно критика в адрес этого понятия выражена в словах русского математика А.А. Маркова, одного из наиболее ярких представителей конструктивного анализа. Марков пишет:

            «Мыслить себе бесконечный, т.е. никогда не завершаемый процесс как завершенный не удается без грубого насилия над разумом, отвергающим такие противоречивые фантазии».

             В последние годы в работах выдающегося российского математика и философа Александра Зенкина (1937-2006) [3,4], а также в работах других авторов [5,6] были предприняты радикальные попытки «очищения» математики от канторовской теории бесконечных множеств. Анализ канторовской теории бесконечных множеств, изложенной в статьях [3,4], привел Александра Зенкина к заключению, что доказательства многих теорем Кантора о бесконечных множествах являются логически некорректными, а вся «теория Кантора» в некотором смысле является «величайшей математической мистификацией 19 в.». И выводы Александра Зенкина полностью согласуются с оценкой канторовской теории множеств, данными выдающимися математиками прошлого Кронекером и Пуанкаре.

            Обнаружение парадоксов в канторовской теории бесконечных множеств значительно остудило восторги математиков по поводу этой теории, но окончательную точку в критическом анализе теории Кантора поставил именно Александр Зенкин [3,4]. Он показал, что главной ошибкой Кантора было безоговорочное принятие абстракции актуальной бесконечности, что считается недопустимым в математике. На это обратил внимание еще Аристотель, который первым предупредил о невозможности использования понятия «актуальной бесконечности» в математике ("Infinitum Actu Non Datur").

 Таким образом, «Канторовская теория бесконечных множеств» является ни чем иным, как величайшей математической мистификацией 19-го века, своего рода «математическим шарлатанством», и ее принятие математиками 19-го века, без должного критического анализа, является «стратегической ошибкой» в развитии математики. Если бы Канторовская теория бесконечных множеств была подвергнута серьезному анализу еще в 19-м веке, если бы математики всерьез прислушались к мнению Кронекера и Пуанкаре, возможно, удалось бы избежать возникновения современного кризиса в основаниях математики [1].

5. О моем приобщении к «проблеме бесконечности» и влиянии Георгия Чефранова на мои исследования

Книга «Введение в алгоритмическую теорию измерения» (1977)

            Сразу после защиты докторской диссертации на тему «Синтез оптимальных алгоритмов аналого-цифрового преобразования» (1972) я поставил перед собой задачу написать книгу на эту тему. И такая книга «Введение в алгоритмическую теорию измерения» была опубликована в 1977 г. в издательстве «Советское Радио» [7]. Наибольшей трудностью для меня стало написание Главы 1 «Проблема измерения», в которой я попытался проанализировать все известные направления в «теории измерения», включая «математическую теорию измерения». Здесь я впервые столкнулся с понятием «математической бесконечности». Во время наших длительных вечерних прогулок по улице Чехова (Таганрог) от «профессорского дома», в котором я жил, мимо домика-музея Чехова и до центрального пляжа мы проводили жаркие дискуссии по поводу «математической теории измерения», с которой Чефранов хорошо был знаком и как математик и как философ. И эти дискуссии привели к следующему необычному результату, который был изложен в разделе 1.3.2 «Теоретико-множественная теория измерения» книги [7].

            Меня всегда тянуло к Чефранову, а его, повидимому, ко мне. И на первомайских демонстрациях мы всегда оказывались рядом (см. одну из фотографий).

А.П. Стахов и Г.В. Чефранов

Теоретико-множественная теория измерения

            «Математическая теория измерения» начала создаваться в Древней Греции после открытия «несоизмеримых отрезков». Это открытие вызвало первый кризис в основаниях математики. Для преодоления этого кризиса выдающийся древнегреческий геометр Евдокс предложил «метод исчерпывания», с помощью которого он построил остроумную теорию отношений, лежащую в основе античной теории континуума. "Метод исчерпывания" сыграл выдающуюся роль в развитии математики. Будучи прообразом интегрального исчисления, "метод исчерпывания" позволял античным математикам решать задачи вычисления  объема пирамиды, конуса, шара. В современной математике метод исчерпывания находит свое отражение в одной из «аксиом непрерыности» - аксиоме Евдокса-Архимеда, называемой также аксиомой измерения.

            Аксиома Евдокса-Архимеда («аксиома измерения»): Для любых двух отрезков  A и B (Рис.1) можно найти такое натуральное число n, чтобы

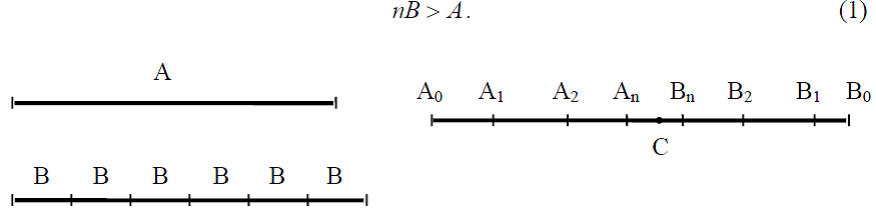
        Рис.1. Аксиома Евдокса-Архимеда                 Рис.2.Аксиома Кантора

           Считается, что свое завершение «математическая теория измерения» получила в 19 в., когда в состав «аксиом непрерывности» была введена «аксиома Кантора»

            Аксиома Кантора (о «стягивающихся отрезках»): Если задана бесконечная последовательность отрезков 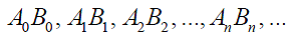 (Рис.2), «вложенных» друг в друга, то есть, каждый отрезок являются частью предыдущего, тогда существует, по крайней мере, одна точка C, общая для всех отрезков.       

Аксиомы Евдокса-Архимеда и Кантора, входящие в состав «аксиом непрерывности», относятся к разряду важнейших геометрических аксиом и составляют методологический базис математической теории измерения, являющейся одним из кирпичей в основании математики.

            Центральным результатом математической теории измерения, основанной на указанных выше аксиомах, является доказательство существования и единственности решения q основного уравнения измерения:

Q = qV,                                                           (2)

где V - единица измерения, Q - измеряемая величина, q - измеряющее ее число.

            Несмотря на кажущуюся простоту сформулированных выше аксиом и всей математической теории измерения, она, тем не менее, является продуктом более чем двухтысячелетнего периода в развитии математики и содержит в себе ряд глубоких математических понятий

Прежде всего, необходимо подчеркнуть, что "метод исчерпывания" и вытекающая из него аксиома измерения имеют практическое (эмпирическое) происхождение; они были позаимствованы древнегреческими математиками в практике измерений. В частности, "метод исчерпывания" является математической моделью процессов измерения объемов жидкостей и сыпучих тел путем "исчерпывания"; аксиома измерения, в свою очередь, концентрирует тысячелетний опыт человека, задолго до возникновения аксиоматического метода в математике миллиарды раз измерявшего расстояния, площади и временные интервалы, и представляет собой сжатую формулировку алгоритма измерения отрезка А с помощью отрезка В. Суть этого алгоритма состоит в последовательном откладывании отрезка В на отрезке А и подсчете числа отрезков В, укладывающихся на отрезке А. В современной практике измерений такой метод измерения называется алгоритмом счета.

Алгоритм счета играет фундаментальную роль в определении самого понятия натурального числа, которое в математике иногда называют "Евклидовым определением":

N = 1 + 1 + … + 1 (N раз)                                                     (3)

Этот же алгоритм лежит в основе таких важных математических понятий как "сложение", "умножение", "деление" и т.д.

            Аксиома Кантора содержит в себе еще одно удивительное достижение математической мысли - абстракцию актуальной бесконечности, о которой рассказывалось выше.

Противоречие между аксиомами Евдокса-Архимеда и Кантора

А теперь я хотел бы рассказать об одном противоречии в основаниях математики, которое было обнаружено мною при анализе аксиом Кантора и Евдокса-Архимеда. Непосредственным толчком для такого анализа стала книга Г.В. Чефранова «Бесконечность и интеллект» [8]. И первым ученым, который одобрил этот неожиданный результат, был Георгий Васильевич Чефранов.

Изучая аксиомы Евдокса-Архимеда и Кантора с точки зрения «актуальной» и «потенциальной» бесконечностей я обнаружил противоречие между ними. Ход моих рассуждений сводился к следующему. Анализ этих аксиом показывает, что аксиомы Евдокса-Архимеда и Кантора основаны на различных представлениях о бесконечном: аксиома Евдокса-Архимеда основана на использовании понятия «потенциальной» бесконечности, в то время как аксиома Кантора – на использовании понятия «актуальной» бесконечности, то есть, между этими аксиомами, лежащими в основе теории действительных чисел, существует противоречие «актуальной» и «потенциальной» бесконечностей.

Более того. Мне показалось, что, вводя свою аксиому, Кантор "слукавил". Действительно, в своей аксиоме он обращается к интуитивно ясному понятию "стягивающихся" отрезков, которое, в свою очередь, основывается на интуитивно ясном утверждении: "часть меньше целого" (каждый "стягивающийся" отрезок меньше предыдущего). Затем, с использованием своей аксиомы Кантор строит свою теорию бесконечных множеств, в которой он доказывает противоположное, то есть "часть равномощна к целому", что находится в противоречии с допущением, принятом в «аксиоме о «стягивающихся" отрезках». Но если в основаниях теории действительных чисел (математическая теория измерения) заложены аксиомы, противоречащие друг другу, то и сама теория действительных чисел является противоречивой, что и выражается в современном кризисе в основаниях математики.

В своей книге [7] я выразил эту идею в следующих словах:

«Для пояснения различий между двумя толковаиями бесконечного еще раз обратимся к аксиомам Кнтора и Архимеда. В аксиоме Кантора вся бесконечная совокупность «стягивающихся» отрезков вместе с объединяющей их точкой считается заданной всеми своими объектами одновременно, - допущение таких «завершенных» бесконечных совокупностей и является наиболее характерной чертой теортико-множественного стиля математического мышления. Аксиома Архимеда, имеющая эмпирическое происхождение, является примером конструктивной аксиомы и «в неяном виде опирается на на абстакцию потенциальной осуществимости, поскольку предполагает после каждого шага процесса возможность построения отрезка, большего, чем предыдущий» ([9], c.137). Число шагов измерения в аксиоме Архимеда, необходимое для выполнения условия nB>A, всегда конечно, но потенциально неограниченно; в этом и состоитконструтивное понимание бесконечности как потенциальной, «становящейся» категории. В этой связи уместно обратить внимание на внутреннюю противоречивость (в диалектическом смысле) теоретико-множественной теории измерения (и как следствие теории действительных чисел), допускающей в своих исходных положениях (аксиомы непрерывности) сосуществование диалектически противоречивых представлений о бесконечном (актуальной, «статической», завершенной бесконечности – в аксиоме Кантора ... и бесконечности потенциальной, «становящейся – в аксиоме Архимеда)».

Но ведь это – катастрофа для математики: в основаниях математики («аксиомы непрерывности») используются аксиомы, которые являются взаимно противоречивыми. Отсюда вытекает, что вся теория действительных чисел, а следовательно, и вся математика являются противоречивыми! Это означает, что с момента введения аксиомы Кантора (1872 г.) математика превратилась в противоречивую теорию! И эти ужасающие противоречия обнаружились в математике в начале 20 в. [1].

Переписка с А.Н. Колмогоровым

Я поделился своими рассуждениями с доктором философских наук и профессиональным математиком Георгием Васильевичем Чефрановым, и он не нашел в них какого-либо изъяна. Он воспринял эти идеи с большим энтузиазмом, усматриваля в них серьезный математический результат, касающийся оснований математики, и он решительно порекомендовал мне обратиться к академику А.Н. Колмогорову.

По совету Чефранова я написал о своих идеях академику А.Н. Колмогорову. Колмогоров в своем ответе попытался опровергнуть мои рассуждения. Поскольку его ответ меня не удовлетворил, я попытался в одну из моих очередных поездок в Москву встретиться с академиком Колмогоровым. К сожалению, выдающийся математик встретил меня не очень приветливо, то есть, серьезного разговора не получилось. Через несколько дней я понял, что причина этого была не во мне, а в той политической ситуации, в которой в тот момент находился Колмогоров. Именно в тот период был пик борьбы КПСС с «диссидентом» Андреем Сахаровым. ЦК КПСС вынуждало академиков подписать «осуждающее» письмо против академика Сахарова (и такое письмо, где была и подпись Колмогорова) было опубликовано. Однако попытка лишить Сахарова ученого звания академика (что решалось путем тайного голосования) не удалась: академики восстали против ЦК КПСС. 

После этого я на многие годы забыл об этом моем увлечении проблемой бесконечности (после переезда в Винницу я занимался реализацией моих зарубежных патентов по «компьютерам Фибоначчи»)  и вспомнил об этом только после того, как встретился с доктором физико-математичких наук проф. Александром Зенкиным во время моей лекции по «математике гармонии», прочитанной мною 29 мая 2003 г. в МГУ на научном семинаре «Геометрия и Физика» (руководитель доктор физико-математических наук, профессор Ю.С. Владимиров).

6. Как я участвовал в «спасении» Г.В. Чефранова

      Георгий Васильевич Чефранов с виду не был эмоциональным человеком и казался даже замкнутым. Он всегда был погружен в свои ведомые лишь ему размышления. Но когда он начинал говорить, он становился эмоциональным человеком; его захлестывали и перехлестывали эмоции. Эрудиция Чефранова была беспредельной. Он знал ВСЕ. И студенты невероятно его любили и восхищались, потому что он был Лектором от Бога. И он иногда говорил такие вещи, о которых говорить было опасно.

Вспоминаю одну историю, связанную с Г.В. Чефрановым, в которой я принимал активное участие. Его лекции и выступления были всегда чрезвычайно интересными и очень острыми (как говорится "на грани фола"). На одной из лекций, прочитанных им в городском "Доме политпросвешения", он провел параллель между Гитлером и Сталиным, назвав их величайшими подонками в истории человечества. Конечно, это сразу же стало известно в Таганрогском горкоме партии, и этот случай сразу же стал предметом серьезного разбирательства по партийной линии. Горком поставил вопрос очень жестко, и дело могло бы закончиться исключением Чефранова из партии и уходом из института. После этого он вряд ли смог бы найти работу по специальности в любом университете Советского Союза.   

Я в то время был членом партийного комитета института и прилагал все усилия, чтобы смягчить ситуацию и не довести дело до исключения из партии. Каждый вечер мы встречались с Георгием Васильевичем и обсуждали, как выйти из создавшейся ситуации. В конечном итоге, партком института принял наиболее мягкое решение и объявил Чефранову строгий выговор с занесением в учетную карточку с формулировкой "за низкое качество лекций". Это решение пошло на утверждение в райком партии. Но здесь произошло  неожиданное событие. Именно в этот период из ВАК СССР Георгий Васильевич получил долгожданное сообщение, что ему присуждена ученая степень доктора философских наук (дело о присуждении Чефранову ученой степени доктора философских наук рассматривалось в ВАКе СССР около 5 лет). Если мне не изменяет память, это был первый доктор философских наук в институте и в городе Таганроге. Перед райкомом встала сложная проблема – утвердить строгий партийный выговор "за низкое качество лекций" доктору философских наук, одному из лучших лекторов института. В конечном итоге, у членов райкома "хватило ума" и "дело Чефранова" было "спущено на тормозах".

Немного истории

По моей иницативе в журнале «Топос» была опубликована уникальная статья Г.В. Чефранова «Числа Фибоначчи и тайны Мироздания» . Эта статья хранилась у меня с 1988 г.

Несколько слов об истории появления этой статьи. Я покинул Таганрогский радиотехнический институт в 1977 г. Меня на это подтолкнул ректор Винницкого политехнического института профессор И.В. Кузьмин, который сагитировал меня на должность зав. кафедрой вычислительной техники вновь созданного Винницкого политехнического института. Позже я очень пожалел об этом решении, потому что в Винницком политехническом институте, по крайней мере, в начальный период, не было такого дружного и высокоинтеллектуального профессорского колектива, как в Таганрогском радиотехническом институте. Наоброт, в профессорской среде царили склоки, подсижывания, анонимные письма и т.д. И самое главное – не было такого уникального ученого как доктор философских наук профессор Чефранов Георгий Васильевич, который оказал огромное влияние на мое научное творчество. Вдали от профессорской среды ТРТИ я чувствовал себя весьма одиноким.

Оказалось, что и после моего ухода из ТРТИ Георгий Васильевич внимательно следил за моими работами и публикациями обо мне.

В 1988 г. в течение двух месяцев (апрель-май) я работал Приглашенным Профессором Дрезденского технического университета. В этот период я прочитал курс лекций «Числа Фибоначчи и компьютеры» для студентов и аспирантов Дрезденского технического университета, а также выступил с докладами по своему научному напрвлению в ряде ведущих университетов и научных учреждений ГДР, в частности, в Техническом университете г. Карлмарксштадт и в Центральном Институте кибернетики и информационных процессов ГДР (Берлин). По результатам моего пребывания в Дрезденском техническом университете я был награжден «Мемориальной Медалью Генриха Баркхаузена». По итогам моего пребывания в ГДР газета «Правда» опубликовала большую статью «Вот вам и Фибоначчи! Стоит ли загонять в тупик новое научное направлеение?» Благодаря этой публикации Академия наук Украины узнала о моих научных результатах. По инициативе ее Президента, академика Б.Е. Патона в июне 1989 г. было организовано специальное заседание Президиума АНУ, посвященное обсуждению моего научного направления.

Эта публикация также вызвала огромный поток писем ко мне со всех концов Советского Союза. И одним из них было письмо Георгия Васильевича Чефранова. Оно называлось «Числа Фибоначчи и тайна Мироздания».

Это письмо Георгий Васильевич, повидимому, написал на основании той инфорации, которую он получил от меня во время наших замечательных вечерних прогулок по ул. Чехова в Таганроге. Ясно, что он был прекрасно ознакомлен с содержанием моих книг «Введение в алгоритмическую теорию измерения» (1977) [7] и «Коды золотой пропорции» (1984) [10].

Я бы выделил несколько наиболее важных идей, которые обсуждаются в статье Чефранова [11].

Числа Фибоначчи как одна из «Тайн Мироздания»

Чефранов пишет:

«Еще Пуанкаре писал о том, что в город под названием "Тайна Мироздания" ведет множество дорог: в этот город можно войти и через заставу музыки, и через заставу математики, и через любые другие частные сферы знаний, - если только вникнуть в них достаточно глубоко! ... Но, само собой разумеется, некоторые заставы могут оказаться более близкими, а некоторые - более далекими от центра этого воображаемого города мировых проблем».

И далее:

«...Ближе к центру того города, о котором писал Пуанкаре, стоит не ребенок, думающий о том, что он думает, и не взрослый, вспоминающий о вечном и бесконечном только на похоронах, а профессор математики, профессионально занимающийся проблемой бесконечности при исследовании чисел Фибоначчи и не чуждый вопросам этики-эстетики. Именно таких математиков, углубляющихся до философских начал мироздания, и философов, способных от общефилософских принципов перейти  к конкретной научной картине мира, имеет в виду статья "Вот вам и Фибоначчи!" в "Правде" от 19.11.88, усматривая в числах Фибоначчи не банальность типа "Дважды два - четыре", а ту простоту пифагорейской гармонии, за которой современная наука обнаруживает и энергетическо-информационный код природы (Ян Гжедзельский), и глобально-космический принцип симметрии (Э.Сороко), и еще многое другое».

            В этой связи уместно вспомнить рассуждения ученого монаха Брата Альфреда Бруссау (Alfred Brousseau), одного из создателей американской Фибоначчи-Ассоциации. Тем, кто изучает числа Фибоначчи, Альфред Бруссау рекомендовал "обращать внимание на поиск эстетического удовлетворения в них. Существует некоторый вид мистической связи между этими числами и Вселенной".

            И еще одна цитата из статьи Чефранова:

            Числа Фибоначчи являются вершиной айсберга тайны мироздания, главным образом, в том смысле,  в каком они являются обобщением "золотого сечения", отражающего фундаментальнейший принцип симметрии, сопричастный, в свою очередь, той гармонии общемирового единства, в которой и кроется информационная тайна мироздания.

            "Золотым сечением" называют такое отношение суммы двух величин к большему слагаемому, которое равно отношению большего слагаемого к меньшему слагаемому. Числа Фибоначчи являются обобщением "золотого сечения", поскольку они фиксируют дальнейшее спиралеобразное развитие пропорциональной зависимости последующей величины от двух предшествующих величин. В реальных спиралеподобных процессах закономерность, найденная Фибоначчи (последующее определяется предыдущим), естественно дополняется закономерностью, найденной Марковым (последующее не зависит от предыдущего), так  как первое исключает появление того, чего раньше не было, т.е. обеспечивает устойчивость, второе исключает влияние предыдущего на последующее, т.е. обеспечивает изменчивость, рождение нового. Поэтому практическое приложение закономерности Фибоначчи концентрируется в сфере измерений высокой точности, т.е. в метрологии. Счетные машины, построенные не на двоичной, десятичной и прочих системах с рациональным основанием, а на системе чисел Фибоначчи, обнаруживает исключительно важное, ни с чем не сравнимое преимущество: способность к самообнаружению ошибок! Построенные на основе систем счисления с иррациональными основаниями типа "золотой пропорции" (кодов Фибоначчи) компьютеры обеспечивают точность при преобразовании поступающих сигналов 99,995 процентов (А.П. Стахов «Синтез оптимальных алгоритмов аналого-цифрового преобразования», Таганрог, 1972; "Коды золотой пропорции", Москва,1984 и другие работы этого же автора, в том числе статья в престижном международном сборнике "Симметрия-2", Нью-Йорк, 1989)».

Обсуждение аксиом Кантора и Архимеда

            Чефранов пишет:

            «Затрагивая вопрос о природе измерения, неизбежно приходят к необходимости проанализировать предпосылки аксиом Архимеда и Кантора, на основании которых эти измерения производятся. Аксиома Архимеда говорит о том, что насколько бы одна величина не была больше другой, повторив меньшую надлежащее число раз, мы превзойдем большую. Тем самым постулируется принцип бесконечного бескачественного деления и увеличения, лежащий в основании учения Гроссмана о протяженности»

            И далее следующее важное замечание:

            «О том, что центральное понятие классической физики, понятие геометрической протяженности, на котором, как на архимедовой точке опоры, стоял последние триста лет мир позитивистской вольтеровско-галилеевской науки (и опиравшийся на него мир политического макиавеллизма), поражено внутренне неразрешимым противоречием, которое знали только математики, да и то не все, а лишь те, которые ясно представляли себе несовместимость аксиом Архимеда и Кантора. Последняя говорит о том, что если на прямой дана бесконечная последовательность вложенных друг в друга отрезков (т.е. таких отрезков, из которых каждый составляет часть предыдущего), то существует по крайней мере одна точка, общая всем этим, - вложенным друг в друга, - отрезкам. Кантор, как и Архимед, предполагает, что понятие протяженности в смысле Грассмана, т.е. возможность ничем не ограниченного бесконечного деления и накопления, является незыблемой предпосылкой научного понимания мира, азбукой рационального образа мыслей, - как об этом сказал еще Декарт, заменивший самоочевидным для здравого смысла понятием протяженности ненаглядное и несамоочевидное информационно-космическое понятие Вселенной как образования более сложного и более информационно-насыщенного, чем человек. По этой причине, на первый взгляд, никакого противоречия между Архимедом и Кантором нет. Этой интерпретации придерживался, например, академик Колмогоров. Но так называемое конструктивистское течение в математике (представленное в СССР именами Макарова-младшего, Новикова, Шанина) исходит из идеи Гильберта о том, что в реальной жизни нигде бесконечное не реализуется, что реальная, работающая, конструктивная, т.е. имеющая с реально осуществляемыми алгоритмами, математика должна отказаться от идеи актуально реализуемой бесконечности, и, следовательно, отказаться от аксиомы Кантора, основанной на допущении реальности именно такого бесконечного процесса. В аксиоме Архимеда речь идет о как угодно большом, но конечном числе, а у Кантора говорится о бесконечном процессе, ведущем к ситуации, где наличествует объект, не имеющий частей, - точка».

            В этом высказывании содержится полная поддержка обнаруженного мною противоречия между аксиомами Кантора и Архимеда, изложенного в книге [7]!

Проблема «информационной Вселенной»

Но в этом письме Чефранов затронул широчайший круг проблем, связанных с развитием современной науки, в частности, проблему «информационной Вселенной». Чефранов пишет:

«И вот Вернадский, Бор, Винер заявили, что не библейским мифом, а основой основ современной науки является статус Информации, Слова, Логоса, аристотелевской Энтелехии не как архитектурного излишества на здании видимой нами Вселенной, а как фундамента этого здания! По Вернадскому интеллект является не случайным огоньком, вспыхнувшем где-то в углу Вселенной, а ноосферой, т.е. такой же закономерной стадией эволюции Космоса, как и образования звезд или галактик. По Винеру информация, масса и энергия являются теми тремя китами, на которых стоит мир. При таком подходе определяющей чертой Универсума является не бесконечная геометрическая кубатура, по отношению к которой даже нельзя ставить вопрос о том, умнее она или глупее человеческого разума, а бесконечная информационная сложность, тот эйнштейновский сверкающий неземной красотой Логос, лишь слабой моделью которого является наш разум. В стремлении хотя бы в общих чертах постигнуть гармонию этого Логоса Эйнштейн видел единственный смысл существования человека!»

Видимо, после «проблемы бесконечности» второй проблемой, которая всегда интересовала Чефранова, являлась «проблема информационной Вселенной». И этому посвящена большая часть его статьи.

            В заключение этого раздела Чефранов написал:

            «Таким образом, из всего вышеизложенного можно сделать только один вывод: без информации, как равноправной (а иногда и ведущей) по отношению к массе и энергии компоненте мироздания, составить себе представление о путях, ведущих к тайне мироздания, сегодня невозможно!»

Несомненно, что в этой статье Георгий Васильевич Чефранов продемонстрировал свою широчайшую научную эрудицию и эта статья является подтверждением его незаурядности.

И я горжусь тем, что судьба свела меня с этим уникальным ученым, который оказал огромное влияние на мое научное творчество.

1. Клайн М. Математика. Утрата определенности (пер. с англ.). Москва: Мир, 1984. 434 с.
2. Марков А.А. О логике конструктивной математики. М.: Знание, 1972.
3. Zenkin A.A. Super-Induction Method: Logical Akupuncture of Mathematical Infinity. - Twentieth World Congress of Philosophy. Boston, U.S.A., 1998. Proceedings, Section "Logic and Philosophy of Logic."
4. Зенкин А.А. Ошибка Георга Кантора // Вопросы философии. 2000, №2.
5. Стахов А.П., Клещев Д.С., Проблема бесконечного в математике и философии от Аристотеля до А.Зенкина // «Академия Тринитаризма», М., Эл № 77-6567, публ.15680, 03.12.2009
6. А.П. Стахов, Не стоит ли современная математика на «лженаучном» фундаменте? (В порядке обсуждения статьи Дениса Клещева «Лженаука: болезнь, которую некому лечить») // «Академия Тринитаризма», М., Эл № 77-6567, публ.17034, 28.11.2011 
7. Стахов А.П. Введение в алгоритмическую теорию измерения. М.: Советское Радио, 1977.
8. Чефранов Г.В. Бесконечность и интеллект. Ростов: Изд-во Ростовского госуд. ун-та, 1971 г.
9. Рузавин Г.И. О природе математического знания. М.: Мысль, 1968.
10.  Стахов А.П. Коды золотой пропорции. М.: Радио и связь, 1984.
11. Чефранов Г.В. Числа Фибоначчи и тайны Мироздания. Журнал «Топос», 2013